Copyright ©Tatar 2006
I have spent many years proceeding with a research programme in which coordinated activities were seen as the key to engagement and engagement the key to learning. However, in recent years a new element has entered the equation: demonstrations of impact.
My first job out of college was at the Logo Lab at M.I.T.. Logo was a computer language for children and an associated way of thinking. It, and Scheme, and Boxer, changed my life. Arguably, changing my life is of little significance. There is a considerable gap between "it changed my life," and "it would change other people's lives, and enable excellence or avoid inequity" and yet another gap between "it changed my life" and "it would change everybody's lives."
An innovation that is oversold can leave good people disappointed and tax the resources of well-intentioned schools, teachers and students. One has to ask, as a parent did at a professional ACM meeting recently, "Why should my school invest in computers for math when they can't even afford art?"
This is an excellent question, and one that requires a serious answer.
Part of the answer is why I take SimCalc seriously. Like Logo, SimCalc is another technology for learning, devolving from the representational innovations of the cognitive revolution. It allows students to gain a visceral as well as intellectual understanding of the math of change and variation (especially algebra). It has been used with tremendous success with about 1000 students in some of the most challenging schools in the United States,including those in urban Newark N.J. (Roberta Schorr); San Diego California (Janet Bowers and Susan Nickerson); and the worst performing high schools in Massachusetts (the late Jim Kaput and Stephen Hegedus). It has also been used in high performing classrooms and schools (see handheld math).
 |
|---|
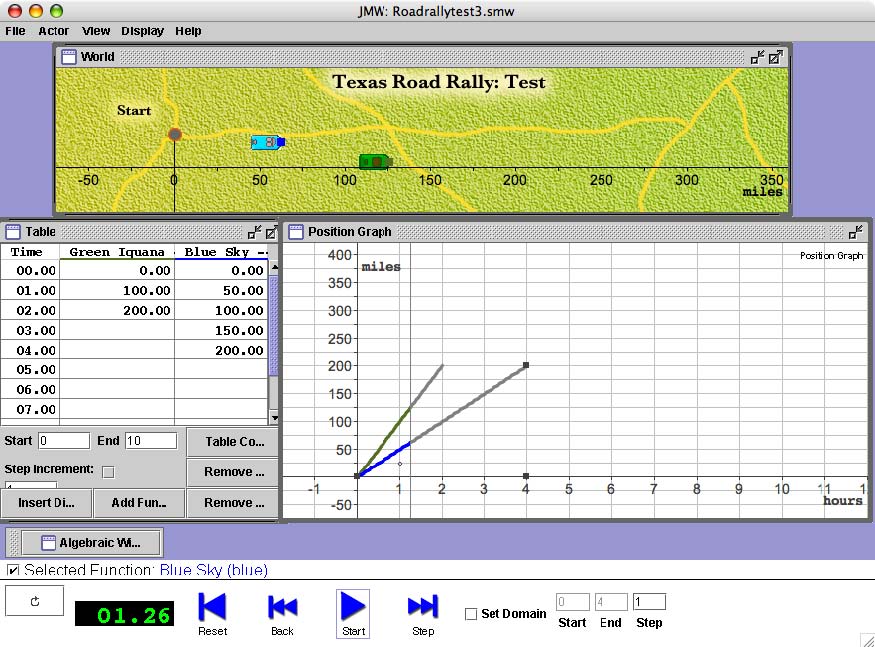
| One view of SimCalc. At the top is the simulation area or "world". In the middle, on the left is a table view of the data. On the right is a position graph. Below, the algebraic view is shrunken. The controllers appear at the bottom of the window. No velocity graph appears here at all, as the students have not yet encountered representations of velocity. |
But this is only one kind of evidence, not enough for large-scale adoption. We would like more, with more certainty. As the professor in my methods class, the great experimental psychologist Claude Steele, commented one day, controlled experimentation is the "most esteemed" form of coming to know about the world.
So rigorous controlled experimentation is desirable. But rigorous controlled experimentation rests on certain assumptions that cannot always be met. Few have developed rigorous meta-theories about the nature of knowing as we slide from perfect to imperfect conditions. Even in psychology, experimentation is often performed on a select sample of students.
In the Scaling Up SimCalc project, we are taking on the challenge of exploring the gap between working in the small and working in a more general context, utilizing the tool of controlled experimentation. Our general hypothesis is that a wide variety of teachers can learn to teach successfully with this technology and associated curriculum compared to their success with other possible interventions.
Our pilot study involved 23 7th grade math teachers in Texas, utlizing a three week replacement unit on rate and proportionality. Half were randomly assigned to the SimCalc condition and half to a control condition involving a very nice approach to teaching rate and proportionality without technology. It was highly successful.
We are currently analyzing the first of a follow-on experiment with 95 7th grade math teachers in Texas, running the secondf year, and running an additional study with 80 8th grade math teachers.
Alternative approaches to structuring knowledge acquisition made possible by handheld architectures represent a significant opportunity to change the participatory structure of learning in technical areas.
Two papers report the design, implementation and results of the study so far:
Tatar, D., Roschelle, J., Knudsen, J., Shechtman, N., Kaput, J. & Hopkins, B. (in press) Scaling Up Innovative Technology-Based Math. Journal of the Learning Sciences.
Roschelle, J., Tatar, D. and Kaput, J. (in press) Getting to scale with innovations that deeply restructure how students come to know mathematics and science. In Kelly, E. A. and Lesh, R. (Eds.) Handbook of design research in mathematics, science and technology education. Mahwah, NJ: Erlbaum.
Please see publications page for any downloads.