CS 4604 Homework #3 Solution Sketches

(10 points) Here are two possible diagrams. Any answer where either S or T inherits from R is plain wrong since then the keys cannot be different (but the question says they are different). Any answer where R, S, or T is a double diamond is also wrong because we never create relations for double diamonds (and even if we did, it wouldn't really match the signature provided in the question).

(In the second diagram, as in the first, the attribute for S is a "d"; the drawing may not be clear when printed)
(10 points) The ODL schema can be given by:
```
class R 
(key a)
{
	attribute integer a;
	relationship Set<V> RtoV
		inverse V::VtoR;
};

class S
(key b)
{
	attribute integer b;
	relationship Set<V> StoV
		inverse V::VtoS;
};

class T
(key c)
{
	attribute integer c;
	relationship Set<V> TtoV
		inverse V::VtoT;
};

class U
(key d)
{
	attribute integer d;
	relationship Set<V> UtoV
		inverse V::VtoU;
};

class V
(key VtoR VtoS VtoT VtoU)
{
	relationship R VtoR
	     inverse R::RtoV
	relationship S VtoS
	     inverse S::StoV
	relationship T VtoT
	     inverse T::TtoV
	relationship U VtoU
	     inverse U::UtoV
};
```
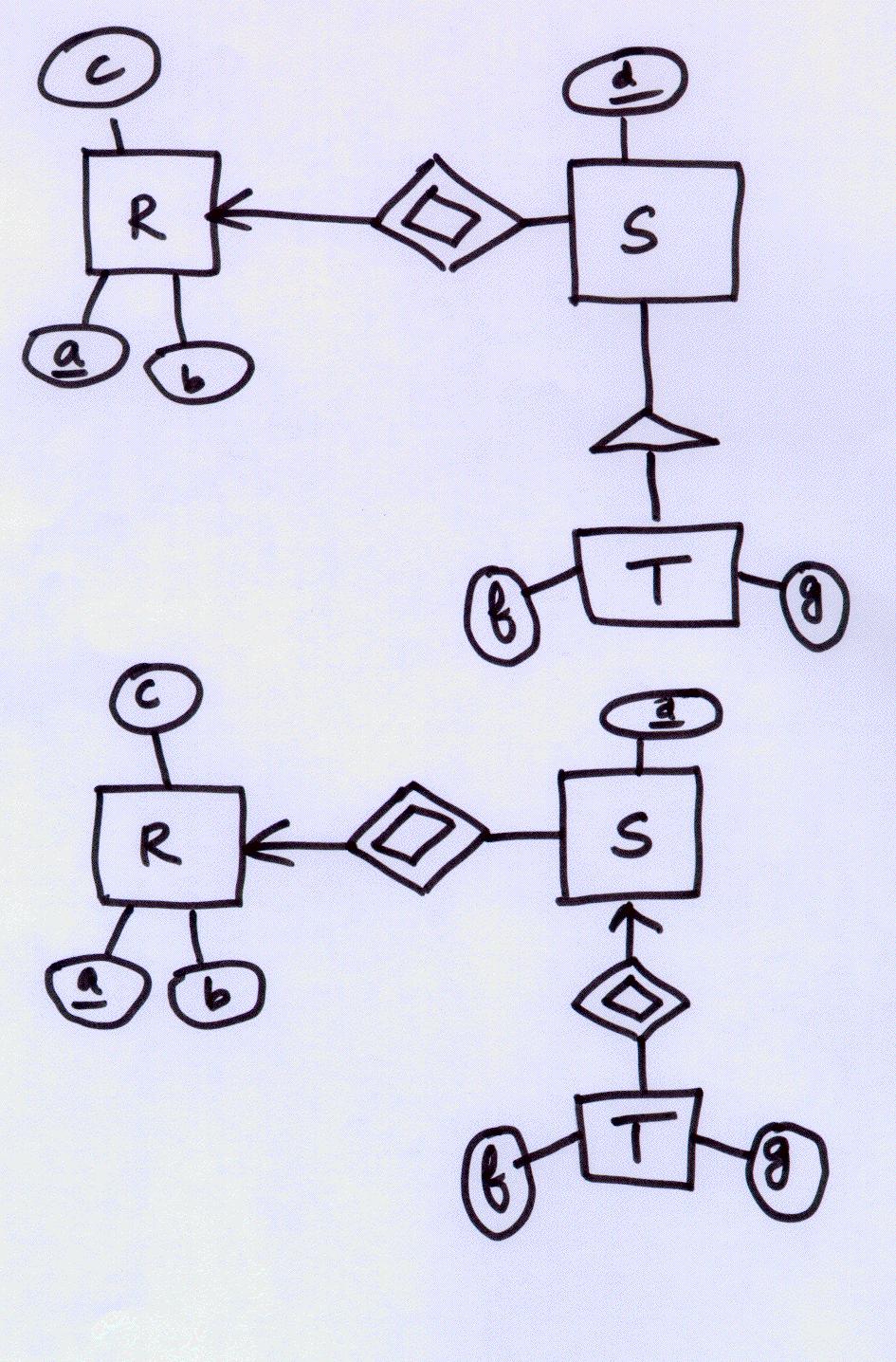
V is the type of class that would have been obtained via a pushed-out E/R diagram (i.e., V would be a multiway relationship between R, S, T, and U; after the push-out it would become an entity set with many-one relationships to each of the other four entity sets). Recall that we cannot have multiway relationships in ODL and so we would have employed the push-out construction to render the diagram in ODL.

In E/R terms, V would be a weak set since it is dependent on all of R, S, and T, and U to contribute towards its key. Recall that one of the main causes of weak sets is the push-out construction. In fact, we can go one step further and also say that not only is V resulting from the push-out of a multiway relationship, but that the multiway must have been many-many in all directions (i.e., it doesn't have any arrows). This is because all four attributes are used to form the key for V. If there was at least one arrow, there would have been a key possible with only three attributes (not four). The question indicates that all four attributes make up the key for V, so we can make this inference (see diagram below).

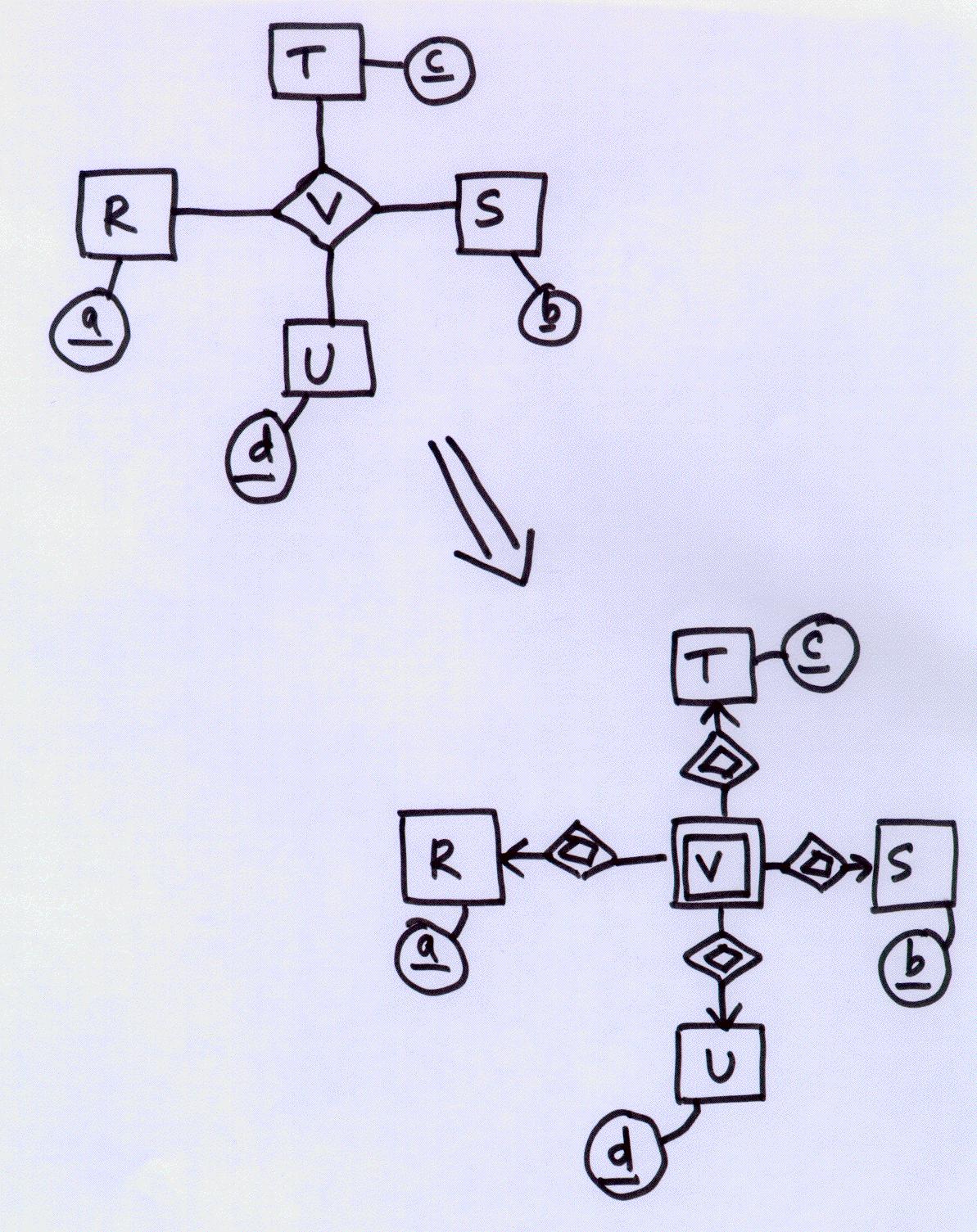
Full points if you gave the correct ODL code and also made the inference about the push-out of a many-many-many-many multiway relationship. 8 points if you only give the ODL code, without the inference. 9 points if you give the ODL code, make the inference about the push-out, but not about the many-many-many multiway relationship.
(5 points) Any superkey has to contain A1, A2, or both. The only points of leverage are the remaining attributes (of which there are (n-2)). These remaining attributes need or need not be present (we don't care!). The number of ways in which we don't care is 2^(n-2). Since there are three ways to use these don't cares to create superkeys (i.e., either add A1, or add A2, or add both), the total number of superkeys is 3*2^(n-2).

Another way to calculate this is as follows: The number of superkeys that have A1 is 2^(n-1). The number of superkeys that have A2 is 2^(n-1). If we add them, we get 2*2^(n-1). But we would have counted some of these superkeys twice. The precise number we double-counted are the ones that have both A1 and A2. So, we have to subtract these superkeys, of which there are 2^(n-2) (since they have both A1 and A2 in them). So, the final answer is: 2*2^(n-1) - 2^(n-2), or just 2^n - 2^(n-2).

In case you haven't figured it out, this is just the same as 3*2^(n-2). This is because 2^n is equal to 4*2^(n-2).
(5 points) The only way we will know for sure if we got all the FDs is to compute closures of all subsets of S (we take the closure with respect to the original relation R, to make sure we don't miss anything; of course we can always throw away the attributes that are not in S).
```
Closure of A = {A,D} 
Closure of B = {B} 
Closure of C = {C}
Closure of AB = {A,B,D,E}
Closure of AC = {A,C,D,E,B} This gives AC->B
Closure of BC = {B,C}
```
Thus, the only FD we can state for S is AC->B.
(10 points; 2.5 points for each step) We need to first determine the key(s). Notice that A, B and E do not appear on the right side of any FD. Therefore, they have got to be part of a key. Let us see if {A,B,E} by itself could be the key. The closure of {A,B,E} = {A,B,C,D,E}. Thus, indeed the only key is {A,B,E}.
1. We first need to systematically determine all the FDs that hold in R. This is done by computing the closures of all subsets of R. If you do this meticulously, you will notice that you will get an additional FD BE->C. The FDs that are in violation of BCNF are all of them (!), since they do not have a superkey on the left. In other words, the violating FDs are:
```
AB->C
DE->C
B->D
BE->C
```
2. Let us try to decompose it by the first FD: AB->C. We get {A,B,C},{A,B,D,E}. In {A,B,C}, the only FD that holds in AB->C. Since AB is the key, there is no violation of BCNF. In {A,B,D,E}, the FD B->D is in violation of BCNF. We decompose it further to obtain {B,D},{B,A,E}. Each of these is in BCNF (why?). The final relations are therefore {{A,B,C},{B,D},{A,B,E}}.
3. All the original FDs are in violation of 3NF too, since in addition to none of the left hand sides being a superkey, none of the right hand sides has part of a key.
4. Assume that we decompose by B->D. We get {{B,D},{B,A,C,E}}. In the second schema AB->C, BE->C hold. The key is still {A,B,E}. Both are in violation of 3NF. Lets decompose via AB->C. We get {{A,B,C},{A,B,E}}. Each of these is in 3NF. The final schemas are {{B,D},{A,B,C},{A,B,E}}.
  
  A diligent student pointed out that this decomposition does not preserve dependencies (notice that BE->C and DE->C cannot be preserved without a complicated "joining" back of the relations), though we learnt in class that 3NF is good at preserving FDs. The actual algorithm for performing a dependency preserving decomposition is beyond the scope of this course. If interested, please meet the instructor. The itty-bitty-dirty fix to this problem is to add another schema {B,C,D,E} that helps us preserve both the FDs BE->C and DE->C. (In other words, before tuples are added to the other schemas, this schema will ensure that the FDs are preserved).
(5 points) An instance of R for which the given decomposition is lossy would be:
```
a1 b1 c1
a2 b1 c2
```
Decomposing it, we get:
```
a1 b1
a2 b1
```
and
```
b1 c1
b1 c2
```
Joining them back gives, instead:
```
a1 b1 c1
a1 b1 c2
a2 b1 c1
a2 b1 c2
```
i.e., we get two extra tuples. The decomposition is thus lossy. How did we arrive at this example? Notice how we did the decomposition. We performed it based on the assumption that either B->C or B->A holds. We have designed the example (cleverly) to ensure that both of these FDs ~~are violated~~ do not hold. There is no way we will get the original tuples back by performing a decomposition based on an FD(s) that do not even hold in the first place!
(5 points) Notice again that the splitting is not being performed according to the normal rules of BCNF. If the FD A->B is indeed in violation, we should get the relational schemas as {A,B}, {A,C} and not {A,B}, {B,C}. The only way in which this decomposition could be lossless would be if it was performed on the lines of some other ~~violating~~ FD. Since they share the B attribute, the only choices we have are: B->A or B->C. Let's pick B->C as the ~~violating~~ FD. We thus have two FDs for the relation: {A->B, B->C}. The key would be {A}. The second FD is indeed in violation of BCNF (as planned) since its left hand side is not a superkey. An example instance would thus be:
```
a1 b1 c1
a2 b2 c2
a3 b2 c2
a4 b1 c1
```
If you started with the other FD, you will get a solution of a different type.