CS 5614 Homework #3

Solution Sketches
  1. The question introduces the notion of "closed sets" of attributes w.r.t. a given set of FDs. The idea is to figure out what the FDs are.
    • If all sets of the four attributes are closed, there are no nontrivial FDs. Why? Assume that there does exist a nontrivial FD X->Y. Then X's closure contains Y. X is therefore, not closed. Proof by contradiction.
    • For this case, there is not a unique solution. There are many "solutions", each of them being a set of FDs. One possible solution is {A->B, B->C, C->D, D->A}. Another solution is {A->BC, B->CD, C->DA, D->AB} etc. Note that your solution cannot possibly be {AB->C, BC->D, CD->A, AD->C}, because that indirectly assumes that the singleton subsets are closed, which is not the case.
    • Notice that {A} and {B} are not closed, but that {A,B} is. Therefore A->B and B->A have to be present in your solution (why?). Also notice that {C}, {D}, {A,C} etc. are not closed. What exactly you do with these attributes will affect the final solution. One possible solution is {A->B, B->A, C->D, D->C, D->A}.

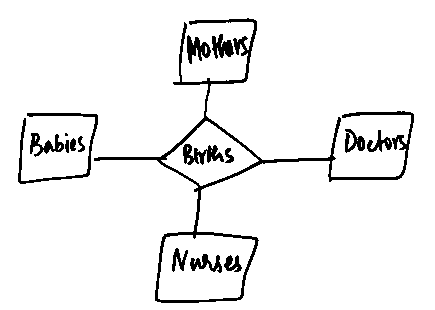
  2. The original diagram mentioned in the question is:

    1. The answer to part (1) is:

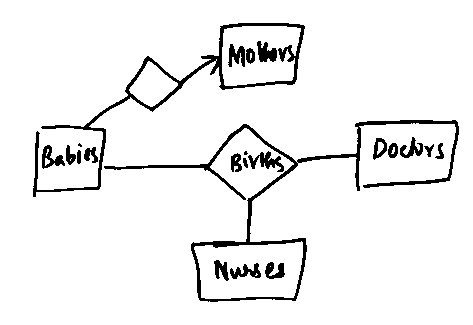
    2. The answer to part (2) is:

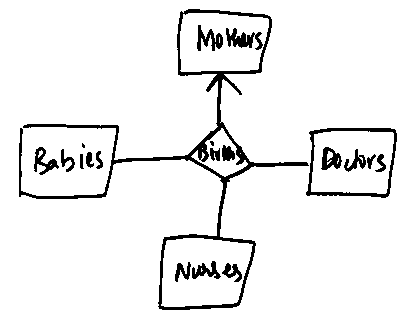
    3. The answer to part (3) is:

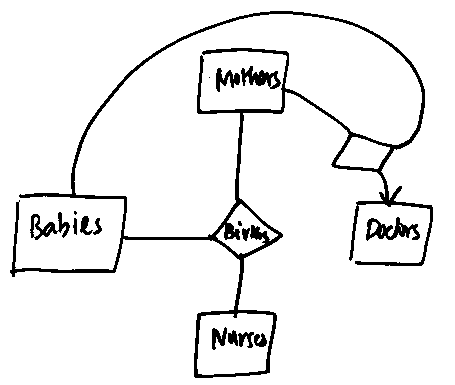
    4. The answer to part (4) is given below. Notice that now births takes on an "existence" of its own; it thus has to become an entity set; we can easily do it by "pushing-out" and then enforcing the additional constraints given in the question. If you made "Births" to be a weak-set, you will not lose points. But make sure, that the key(s) for Births are consistent with the constraints given in the question.

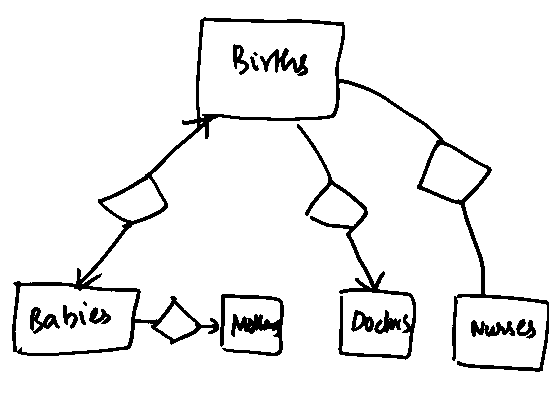
    5. Similarly for the last part. Notice that all we do here compared to the previous part is to remove some potential arrows. A first attempt results in:

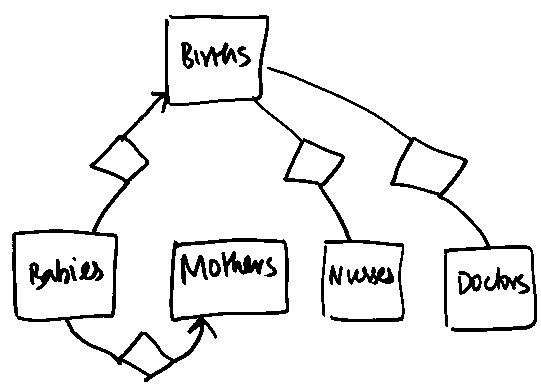      However, this diagram allows tuples of the form: 
      Birth1  Baby1  Mother1
Birth1  Baby2  Mother1
Birth2  Baby3  Mother2
Birth1  Baby4  Mother3
      Notice the last tuple which shows that a Birth can involve more than one Mother. This is obviously not what the question intends - a common sense judgement-call (Courtesy Batul Mirza). One attempt at revision would be to introduce a many-one relationship from Births to Mothers, like so: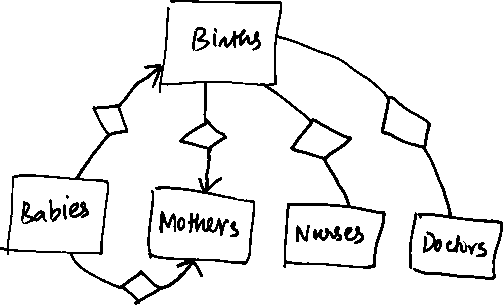

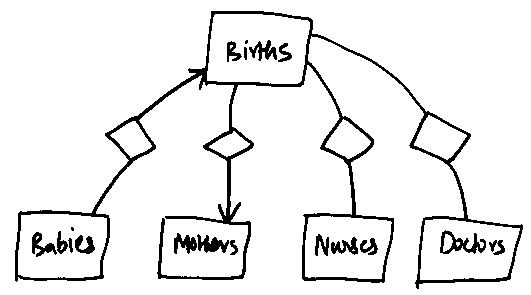
      However, this causes redundancy. We thus remove the many-one from Babies to Mothers (since we can get to a mother anyway through the Birth set). Notice that a many-one relationship from A to B and a many-one from B to C implies a many-one from A to C. The final diagram thus becomes:

  3. This is easily shown by contradiction. Assume that it is not true. Thus, the closure of X contains some attribute Z, which is not contained in the closure of Y. Thus, X->Z is a correct example of an FD. Using Armstrong's second axiom (of augmentation), let us augment both sides of this FD by the set of attributes in (Y-X). Since X is a subset of Y, we thus get Y->(Y-X) U Z. From which, we can derive the FD Y->Z. Thus, Z is present in the closure of Y. Q.E.D.

  4. The first thing to do is to figure out "linear in what?"! A good way to analyze the complexity of such an algorithm is w.r.t. the size of the set of FDs it processes. Since all we have to do is to see if a given FD X->Y holds, we could try computing the closure of X and see if Y occurs in this set. The naive way to do this is to start with an empty set (as the closure of X) and keep adding attributes to it (using some FD) until it stops changing. This is the algorithm presented in Fig. 6.7 in the boat book, Fig. 15.6 in the cow book, and is reproduced here: 
    
Algorithm Naive-Closure
Answer = {X}
Do
   Foreach FD A->B in the given set
	If A is a subset of Answer, then Answer = Answer U B
Until Answer doesn't change (how would you determine this?)
    It is easy to see that you might need to do two complete "sweeps" in the worst-case, leading to a quadratic time algorithm. The intuition behind the linear time algorithm is as follows: You take some extra space to "preprocess" the given set of FDs so that each FD gets "fired" at exactly the right moment when you have all the attributes on the left hand side of it. To do this efficiently, you need to first precompute two functions, one from attributes to the FDs they can help "fire" and another from FDs to the number of attributes that are needed to "fire" them (a running counter). This is to save us a lot of overhead in book-keeping. We present these in a pseudo-C fashion:

    1. FD* atof( ATTR a) is a function that takes an attribute "a" as input and spits out a list of FDs for which "a" appears on the left hand side. Notice that this function can be "designed" in O(nm) time, where "n" is the number of FDs and "m" is the number of attributes. How?

    2. int ftoa[FD f] is an array (a function in the mathematical sense) indexed by FDs (like an FD-id). In other words, it takes an FD as input and returns the number of attributes on the left hand side of the FD. This function can be "designed" in O(n) time. Initially this array will contain the full number of attributes needed to fire, which we will decrement as we keep adding attributes to our closure. Neat!

    Now, the algorithm can be given as: 
    
Answer = {};
Algorithm Closure
Foreach attribute "a" in X
	Answer = Answer U {a};
	Foreach FD f in atof(a) 
		ftoa[f] = ftoa[f] - 1; /* why? */
	        /* check if it is ready to fire */
		if (ftoa[f] == 0) {
			Closure(Y) where Y is the right hand side of FD f;
		}
    Why does this work? If you traverse it carefully, you will see that this algorithm is being really selective in the order of FDs that it fires and how it adds attributes. Moreover, once fired, an FD is never used again. It is thus linear in the size of the FDs (which is the sum total of the attributes in each of the FDs). We leave this proof to the reader (it is a simple complexity analysis of a recurrence equation). Also notice the tail-recursive nature of the algorithm; the recursion can be elegantly removed if this is an issue.

Return Home