(Uma Thurman, Mad Dog and Glory)
(Robert De Niro, Cape Fear)
(Woody Harrelson, Natural Born Killers)
(Dan Aykroyd, The Actor)
(Judge Reinhold, Beverly Hills Cop)
(Jamie Lee Curtis, True Lies)
(Woody Harrelson, Palmetto)
(Nick Nolte, 48 Hours)
(James Russo, Beverly Hills Cop)
(Eddie Murphy, 48 Hours)
(Jamie Lee Curtis, Perfect)
(Tommy Lee Jones, Natural Born Killers)
(Dan Aykroyd, North)
(Tara King, 48 Hours)
(Robert De Niro, Sleepers)
(Nick Nolte, Cape Fear)
(Juliette Lewis, Natural Born Killers)
(Jessica Lange, Cape Fear)
(Eddie Murphy, Beverly Hills Cop)
(Robert De Niro, Mad Dog and Glory)
(Robert Downey Jr., Natural Born Killers)
(Eddie Murphy, Trading Places)
(Juliette Lewis, Cape Fear)
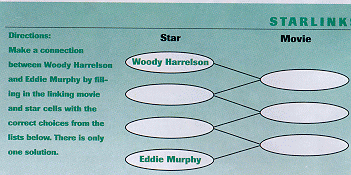
Your task is to make a connection between Woody Harrelson and Eddie Murphy, using *ONLY* the data shown above. Of course, you realize that we are not really worried about how these two are related (in the totality of real-life data), but to see if you can effect the connection via an SQL query. So, use the diagram below; your goal is to fill out the missing two star names and three movie names. To do that, you need to write an SQL query and run it only on the data shown above (again, we are not interested in "complete and real" data, only the results on the data shown above). For full credit, submit your SQL query and the result that you get. To do this exercise, you need to actually sit in front of the computer, load the data, write the query and report on the answer (HINT: There is only one solution). FAQ: I found a "shorter path" between these two actors!!! Is that okay?
Answer: No, that is not okay. Pl. realize that our goal is not to mine the relationships among actors but to learn some database stuff. Your answer should contain exactly three movies and two actors. FAQ: I found the answer, just by looking at it. Is that okay?
Answer: No, again. We need the SQL query.
Write a program in your favorite programming language (C/C++/Perl etc.) that determines an optimal join strategy for computing "R1 Join R2 .... Rn". Assume that all relations are of size 1000. The program will take as input the "V" information, for only the "common" attributes (you don't really need any other data). The number of "V"s needed is 2(n-2) + 2. Your program will take them as command line arguments. For example, one invocation of your program would be:
> my_algorithm 200 100 500 20
This attempts to do a join of three relations: R(X,Y), S(Y,Z), T(Z,L), where #(R) = #(S) = #(Y) = 1000, and V(R,Y) = 200, V(S,Y) = 100, V(S,Z) = 500 and V(T,Z) = 20. You can restrict your answer to only left-deep joins. Your program should output two "groupings":
- The grouping obtained by a dynamic programming search
- The grouping obtained by a greedy search
In each case, output your answer with suitable parentheses and/or indentation. For example, for the above "run", the answer should be:
Dynamic Programming Ordering: ((R2 Join R3) Join R1)
Greedy Ordering: ((R2 Join R3) Join R1)
(In this case, they are the same, but you cannot generally assume that they are identical). Recall that the dynamic programming approach searches through all possible O(n!) combinations for left-deep trees and picks out the ones that are "cheapest". What does "cheapest" mean? Recall again that cost of a join is the sum of the sizes of all the intermediate relations considered. The greedy algorithm, on the other hand, picks the two relations whose estimated join is smallest, then incrementally adds relations (such that the join size is minimized) at each step. It thus makes local decisions at every time. As another example, the answer for:
> my_algorithm 200 100 500 20 50 1000
is:
Dynamic Programming Ordering: (((R3 Join R4) Join R2) Join R1)
Greedy Ordering: (((R3 Join R4) Join R2) Join R1)
Again, notice that the greedy answer is the same as the DP one, but this is not generally the case.
What you should turnin: A location on the csgrad lab machines, in your home directory, where we can go and test out this ".exe" file. You are welcome to improvise as much as you want, so long as you satisfy the stated requirements. We will not provide the "data" (nor tell you how many "n"s there are going to be) on which we are going to test your program beforehand, but feel free to exchange test data (not code!) among yourselves. FAQ: This question is downright sadistic! What is the point in asking us to implement this painful program?
Answer: Our goal here is to give you an appreciation for how a query compiler chooses a logical plan. The actual code doesn't take more than 2 pages of any high level lang. code. It is our belief that the only way to "gain this appreciation"is to get your hands dirty and code this up. (You may have some surprises when you go from three relations to four relations)
