Discussion Notes

Feb 02, 2001

Everything is a Matrix (IR and NA viewpoints)

• term-document matrix in IR
  

• people-artifacts matrix in RS
  

• hyperlink matrix in web modeling
  

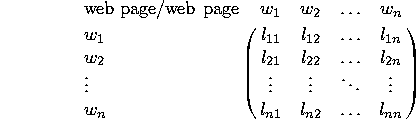
Some points to note about the above formulations

• Choice of terms, documents etc. is very domain-specific. For example, stemming and stopwords are commonly accepted as pre-processing steps in IR to obtain a "good" term-list.
• The first two matrices are typically very lopsided. For example, in IR, or
  
• What do we put inside the matrices: (i) a zero if not applicable (term doesn't appear in document, person doesn't rate artifact etc.), (ii) the non-zero entries can denote various properties of the "presence", such as frequency, inverse frequency etc. There is ages of literature pertaining to what is the "right" way to capture the non-zero entries.
• The web matrix is square and typically not symmetric.
• All three types of matrices are usually 99.9% sparse!

What can we do with these matrices?

• Answer a query
• Study the space (spanned by the vectors of the matrix)
• Study the effect of the matrix in this space
• Do interesting data mining by tinkering with the matrices

Answer a Query

Vector-Space Model (Salton, 1970s): Documents are represented as vectors of terms. Retrieval corresponds to retrieving document vectors that are "similar" enough to input query vector. Similarity was originally measured by the cosine metric of the angle between vectors. As an example, consider the following three-document and three-term collecton, with a query pertaining to "theory":

The dot-product of two vectors is denoted by:





Thus, the angle between two vectors is given by:



(Document) vectors whose cosine metric is within a threshold (typically > 0.5) are "retrieved." For the above query, documents d1 and d2 would be deemed similar (with d2 being twice as similar).

Some points about this model: (i) Notice that while the dot-product calculation looks cumbersome, the number of entries that have non-zeros in both elements of the product would be very few (these are the ones that would contribute to a non-zero dot product). Still, this can get compute-intensive for higher dimensions. (ii) One simplification that people resort to is to normalize all document vectors (to have length one). (iii) Retrieval is not "exact" (which is desirable). For example, the document does not need to have all the terms in the query to "qualify." However, the vector-space model does not model term-term correlations, so it will not bring documents that are connected in two-steps together. Thus, d3 will not be returned for the query, even though "data structures" have something to do with "theory". Simple fixes to this problem are the term-weighting approaches, and use of a thesaurus (sometimes called a lexicon), that explicitly models such correlations. Still the fundamental problem remains that in the vector-space model, terms are assumed to be independent and orthogonally spanning a space. Finally, (iv) there is a need to compare the query vector with every possible document vector to ensure that no relevant document is left behind (i.e., there is no pre-processing, akin to a lazy approach).

Study the space

GOFLA (Good Old Fashioned Linear Algebra, Strang): To figure out exactly what the terms and documents are saying, we can investigate the space spanned by the term vectors and see what kinds of documents are "representable" in this space:



In this formulation, for instance, a new document such as:



can be represented as 6d1 + d2 +9d3. This is possible, because the three document vectors happen to form the basis for the 3D space. A basis is a notion stricter than a span. The basis vectors are said to be minimally spanning and maximally independent. Removing any vector is possible only under the expense of not being able to "represent" some documents. For example, the following collection:



only spans a 2D space. That is, even though they are 3D vectors, they span only a two-dimensional space. The new document vector cannot expressed as a linear combination of the three vectors, as before. At another extreme, adding additional vectors to the matrix is possible only at the expense of redundancy. The collection:



has a fourth document that adds nothing new to the space (it can itself be expressed as a linear combination of the first three). Making all these notions formal is the mathematical concept of rank, which is the dimension of the space spanned by the column vectors. We say that the rank of a matrix is the same as the dimension of its column space. It is also equal to the dimension of its row space (you can figure out what this means).

The rank of an IR matrix is typically much much smaller than either of the two dimensions (terms or documents), since there will be some redundancy among the vectors in the matrix.

Analyze the effect of the matrix in the space

In other words, an eigenvector and eigenvalue of a matrix are together a summary of the effect of that matrix in a space. For every eigen value, there is actually a family of eigen vectors:



Normally, eigen vectors that are normalized to the unit length are used. Excluding the triviality of zero, eigen values and eigen vectors are obtained by solving:



For the above matrix, one of the eigen values is 6 (figure out the other two!). Some cute things about eigen values and eigen vectors:


• The eigen values of a diagonal matrix are just the diagonal elements.
• The eigen values of an upper triangular (or lower triangular) matrix are (also!) sitting along the diagonal (why?)
• The sum of the eigen values is equal to the sum of the diagonal elements (yes, this holds for any matrix!) and is called the trace of the matrix.
• The product of the eigen values is equal to the determinant of the matrix.

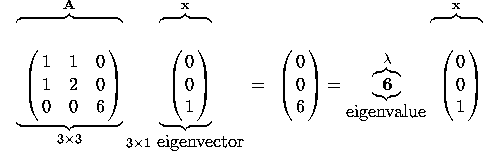
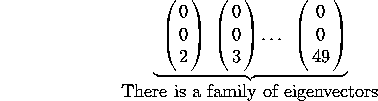
A cute result involving eigen vectors is the following: If you construct a matrix S of the eigen vectors as follows:



then:



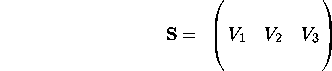
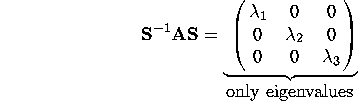
Or, we can think of this as:



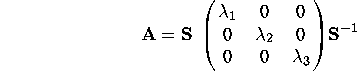
The matrix A is said to be diagonalized. Diagonalization can be thought of as a neat mathematical way to bring about the structure of a matrix. S is sometimes called the eigen-vector matrix and the diagonal matrix of eigen values is sometimes called the eigen-value matrix. Diagonalization is also a way of showing the rank of the matrix explicitly (the number of non-zero diagonal elements in the middle matrix). We are thus introduced to our first decomposition.

Mining Using Matrix Decompositions: A Packaging Analogy

Almost all the papers that we will survey are just different ways of doing this decomposition, by imposing different (and often novel) constraints on the constituent matrices. The nice thing about the decompositions surveyed here (not true of all matrix decompositions) is that they provide a way to "take-apart" the given matrix (A), "throw away" some parts of the matrix, and still "meaningfully" construct an approximation (in a precise mathematical sense) to the original matrix. This packaging analogy is used universally by all the recommender systems papers considered here.

Why these things should work as well as they do, nobody knows.

What we will cover in detail

• SVD: The mother of all decompositions, decompose according to principal components.
• SDD: Overcomes sparsity destroyed by SVD.
• The paper by Booker et al: Decompose-as-you-like-it.
• The paper by Jiang and Littman: a novel way of parameterizing (three) decompositions.
• NMF: An interesting constraint imposed to obtain "additive" factors.
• The CLEVER project: close cousin of the QR decomposition.