Discussion Notes

Feb 05, 2001

Introduction to the SVD

Before plunging into the SVD, it is helpful to consider a close relative of the SVD, applicable to square and symmetric matrices (only). Recall, from last class, that for any matrix A:





In general, notice that the eigen vectors (from different eigen values) that form the S matrix are not orthogonal, but can be chosen to have norm 1. Now, consider this decomposition for a square and symmetric matrix, such as:



The eigen values are easily seen to be zero (nothing special about it) and 5. The eigen vector matrix S is given by:



Notice that the eigen vectors have been normalized to have distance one. Notice that S satisfies the property:



so that the decomposition can be effectively written as:



where Q effectively denotes what we have been calling S so far. It is not an accident that the transpose of the S (Q) also happens to be its inverse. In fact, we can show that all symmetric matrices will satisfy this property for their eigen vectors. In other words, the eigen vectors of a symmetric matrix can be chosen orthogonal (and to have a norm of 1); thus they are said to be orthonormal. Hence a new symbol Q. To extend the above eigen value decomposition to all matrices (not necessarily square and symmetric), we obviously have to make some concessions:


• We can relax the requirement that the left and right matrices be transposes of each other.
  
  
This gives us the singular value decomposition:



Notice that we would still like:



There is a simple way to determine what these matrices should be. Consider two specific cases of using this decomposition:





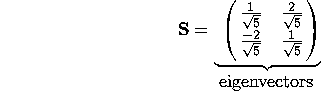
Thus,



and



so that:



The singular value decomposition is thus:



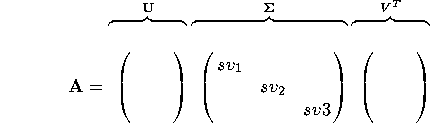
The diagonal elements of are called the singular values (NOT the eigenvalues) of .

Normally the singular values are arranged in decreasing order from top-left to bottom-right. We could drop some percentage of the diagonal values of (replace them with 0), and reconstruct the original matrix. This process can be shown mathematically to give the best rank k approximation to the original matrix A.



Here's a small MATLAB script to tinker with these ideas.

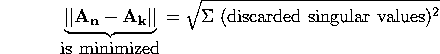
Some points to note aboout the SVD

• SVD models (and helps approximate) both the column space and row space of the original matrix. Thus, it can be used to find term-term correlations, document-document similarities, as well as query for documents using terms as inputs.
  
  
• SVD is better than any "random way" of dropping values (to achieve a lower rank matrix), as the above equality shows. Thus, better is defined in the sense of reducing the Frobenius or the L2 norm. In fact, we can actually derive the SVD based on the constraint that this expression has to be minimized. This is left as an exercise.
  
  
• Why not use the LU decomposition? Answer: there doesn't exist any "meaningful" way in which we can "throw away" something and "repackage" the matrix. SVD provides an intuitive interpretation of "throwing away" and "repackaging".
  
  
• Empirically shown to model synonymy by directly modeling term-term cooccurences. Theory is that it removes noise present in the original dataset by characterizing only the principal dimensions of variability.
  
  
• Intensive to compute; takes time. Lots of research into finding approximate SVDs, and SVDs for special classes of matrices. Heavy influence of parallel computing research.
  
  
• Works well for fairly specific (read long) queries only; cannot ask for exclusions; cannot ask for the decomposition to satisfy any user-specified jumps (fundamentally an ill-conditioned problem).
  
  
• Everything hinges on finding the right number of dimensions to retain - must throw away enough to remove noise and retain enough to not lose any information. Involves empirical tuning for a given collection.
  
  
• The new repackaged matrix can have negative entries; this is counterintuitive, but realize that these are not really document vectors in the original space, they are documents in a new space. So, this is not really a problem. Moreover, since the rank is reduced, and the matrix is not so sparse anymore, there is no way for the basis vectors to remain orthogonal unless some have negative entries.
  
  
• We do not really need to do the repacking for query answering. Can achieve this purpose by projecting the query vector into the new space and using the U and matrices.
  
  
• Other names for SVD: Karhunen-Loeve expansion (signal processing), Principal Component Analysis (statistics).
  
  

LSI = Use of SVD in IR

• Berry's LSI Page at UTK
• Telecordia maintains and distributes LSI "products"
• SVDPACK, for computing the SVD

Leads into next class

• SVD can be used to build indices, since it supports dimensionality reduction. The new dimensions are linear combinations of the original eigen vectors and hence the axes may not have any intuitive interpretation. Moreover, each term no longer occupies a unique dimension. The Booker et al. paper (next class) is a way to overcome this.
  
  
• An undesirable side-effect of using SVD is that it destroys the original sparsity present in A. The SDD paper (next class) is a hack to overcome this.