Aside: An interesting property
- The individual terms are useful as "weightage" coefficients in an infinite
series of updates; the above two properties help to prove convergence results.
The (1/k) sequence
is widely used in neural networks and learning theory, especially
reinforcement learning.
![]()
![]()
SDD
- SDD is an approximate representation of the matrix. Repackaging, even
without removing anything, might not result in the original matrix. Theorems
exist that say that as the number of terms k tends to infinity (!),
slowly you will converge to the original matrix. The speed of convergence
depends on the original estimate, used to "initialize" the iterative
decomposition
algorithm.
- Folding in values in the {-1,0,1} set is somewhat easy, as the authors
point out. Over time, though, folds-in do not work.
- Reduces sparsity and "hey, it works!"
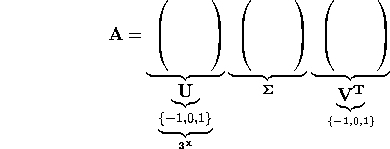
URV
- Does not lock you into principal components and resembles a two-sided
version of QR. U and V still have orthogonal columns. Faster
than SVD to compute, and to update.
- Visualization is given more attention, by allowing user to specify
choices of basis vectors. Need to be careful as users might request
bizarre metrics and choices. Why is this more difficult to do with other
decompositions?
- Cute algorithmic tricks such as centering without "losing sparsity".
![]()
Some interesting observations
- (courtesy Marcos André Gonçalves): Use of the term "noise"
appears to be inconsistent. Sometimes people talk of removing noise, sometimes
"adding noise" to model similarities. This fuzzy notion indicates that
nobody has any clue why these schemes appear to work. Some preliminary work
is reported in the paper
by Papadimitriou et al:
C. Papadimitriou, P. Raghavan, H. Tamaki, and S. Vempala, Latent Semantic Indexing: A Probabilistic Analysis, In Proceedings of PODS'98, 1998.
