Discussion Notes
Feb 14, 2001
(courtesy Aarthi Sundararajan)
The CLEVER project
The Numerical Analysis Viewpoint
We promised that this paper has something to do with matrix
decompositions. The basic "power iteration" described in the article
can be viewed as "one unit" of the QR iteration (which forms
the basis for many factorizations):
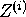 = M
= M 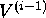
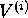 =
=
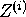
This iteration is guaranteed to converge to the principal eigenvector of M, if (i) the corresponding
eigenvalue 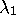 is dominant, i.e., if
is dominant, i.e., if
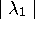 >
> 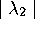
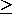
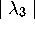 ..........
.......... 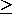
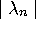
and (ii) the original starting vector V has a component in the direction of this eigen value.
(To ensure that this is satisfied, the authors start with a non-degenerate choice of the eigen
vector, which will have such an entry in all components).
To analyze the convergence properties of this iteration notice that any vector V can be
expressed as:
V = 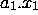 +
+ 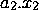 + ......... +
+ ......... + 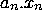
Then, the effect of the iteration above is given by:
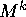 V =
V = 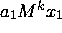 +
+ 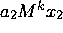 + ......... +
+ ......... + 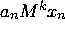
= 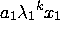 +
+ 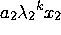 + ......... +
+ ......... + 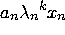
= 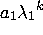 [
[ 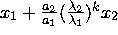 + ....... +
+ ....... + 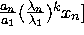
= 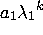 [
[ 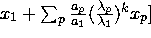
Thus, this iteration converges to the eigenvector corresponding to the largest
eigenvalue with
order of convergence given by:
O( 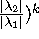 The authors indicate that in their application, convergence is achieved within
a few iterations.
Expanding on this theme, we can make V to be a matrix of two columns, to obtain the
top two eigenvectors. The convergence in this case can be obtained similarly;
except
the ratio of the third and second eigenvalues is taken (instead of the first two).
The full-blown QR iteration obtains all the eigenvectors. The first column of Q would correspond
to the first eigenvector. The second column of Q would correspond to a linear combination of
the first two, and so on.
If M is symmetric (as is the case with the HITS matrix), then we know that
the eigenvalues are real and the eigenvectors can be chosen
orthonormal. In this case, the R matrix of the QR iteration would be diagonal and each of the
columns in Q would be an eigenvector.
The authors indicate that in their application, convergence is achieved within
a few iterations.
Expanding on this theme, we can make V to be a matrix of two columns, to obtain the
top two eigenvectors. The convergence in this case can be obtained similarly;
except
the ratio of the third and second eigenvalues is taken (instead of the first two).
The full-blown QR iteration obtains all the eigenvectors. The first column of Q would correspond
to the first eigenvector. The second column of Q would correspond to a linear combination of
the first two, and so on.
If M is symmetric (as is the case with the HITS matrix), then we know that
the eigenvalues are real and the eigenvectors can be chosen
orthonormal. In this case, the R matrix of the QR iteration would be diagonal and each of the
columns in Q would be an eigenvector.
Other Thoughts
- The main contribution of Kleinberg's algorithm is that a one-mode
graph (of web pages) has actually been viewed in a two-mode context (of hubs and authorities). This
is in contrast to Google and other approaches to modeling web pages. This is probably the most
innovative aspect of the whole study.
- Another selling point is that there are no parameters to tweak, variables to be monitored (other
than the original formation of the matrix).
- One of the disadvantages is that it is query-dependent, analysis cannot be performed offline (as
in Google).
- A lot of engineering goes into making such ideas work, underscores the importance of a large
group to conduct such studies (notice the author list).

