Discussion Notes

Feb 16, 2001

The GraphView

Examples of Graphs

• Bipartite Undirected: Recommendation Datasets
• Unimode Directed: Web
• Unimode Directed: An example is given in the Horting Paper
• Bipartite Directed: ??

Basic Theme in Graphy Papers

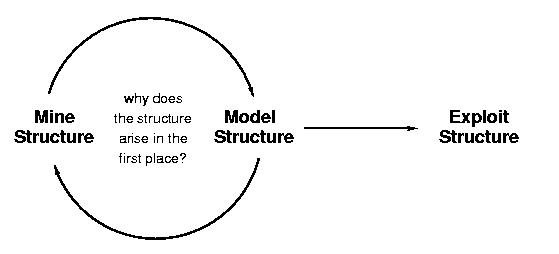
• Mine structure
• Model structure (primarily with random graph models)
• Exploit structure (find/do useful things with it)

Examples of Structures

• Connected? If so, is there a strongly connected component? a clique? a core?
• Disconnected? If so, what do the partitions look like?
• Degree distributions of graphs (frequently cited: power-laws)
• Clustering properties
• Scaling properties
• Replicas, duplicate subtrees
• Small-world behavior
• Hammocks

Algorithmic Viewpoints

• Constructive (construct a shortest-path between X and Y in a given graph)
• Descriptive (characterize the shortest-path in a family of suitably parameterized graphs)
  
  The second approach is the most beneficial for our purposes.

Examples of Models

• Erdos-Renyi (E-R) Model (uniform edge probability)
  • "Almost always" theorems
  • Connectivity constraints
  • Generates Poisson-degree distributed graphs
• Newman-Strogatz-Watts Model (graph-as-you-like-it)
  • Doesn't prohibit multiple edges
• Aiello-Chung-Lu Model (for power-law graphs)
  • Simple like E-R model (only two params)
  • Relatively new, developing
• Watts-Strogatz Model (for small-world graphs)
  • Addresses a specific phenomenon
  • Doesn't model many aspects of typical small-world networks (like degree distribution)

What we can do with models: Two prominent examples

• Find average length between two nodes
• Find the diameter of the graph (max of the min distance across all pairs)

Fundamental Problems with Modeling

• If the structure is hypothesized from specific instances of graphs, how do you know you have captured the "essence" of the graphs? What if the next graph that comes along disproves this?
• Sometimes might need to make distinctions (classic example: Kleinberg's two-mode view of a one-mode graph)
• Sometimes might need to throw away details (literature abounds and revels in this)
• Difficult to ascertain apriori, without looking at lots of specific examples (this is practically impossible for once-upon-a-time graphs like the Web)

Why stuff (structure) happens

• Very little work on this
• Available research inconclusive
• Two examples:
  • Small world graphs: Some evidence from social networks research
  • Power-law graphs: A primary mechanism for achieving robustness (Doyle)