Discussion Notes

(courtesy Ali A Zafer)

starts with a lattice (wreath) which has a high characteristic length and moves towards a random graph through random rewiring. It is important to realize how the careful choice of both the extremes allows the authors to attribute the only cause of length reduction to the newly introduced random links.
To see why this is so delicate, consider another possible kind of rewiring - a preferential rewiring. In this situation, certain nodes have a higher propensity of being linked to. An example of a graph with preferential rewiring is given below:

Lets try to interpolate between the wreath (as the left extreme) and the celebrity graph (at the right extreme). The length reduction comparison in shown below:

As can be seen, in the small p range, the preferential rewirings are virtually indistinguishable from the random rewirings, so the length drops down to similar levels. Only at the high p-range is the difference more stark. It is thus unclear what a good base structure should be to explore the role of preferential links.

Types of links
Growth and death of links
Average degree distribution (see below) doesn't really reflect realistic small-world distributions (notice the authors' assumption of a constant degree for every node). As p increases, the following changes can be seen:
As the rewiring probability increases, the hump manifests itself as the Poisson threshold for a random graph. In many real datasets, the degree distribution looks like a power law.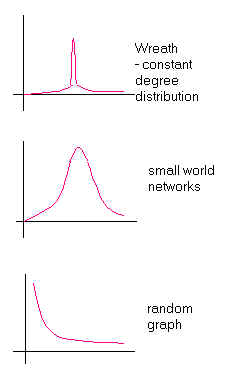
Why people are actually adept at finding short-paths through the network in a distributed manner (some impossibility results from Kleinberg)

Adamic's idea of designing smarter search engines; idea needs to be developed further. Do all distances lie between 2 and 3 (see tables in the paper?)
Gossip spreading
QoS guarantees in networking

mostly a cute model of observed real-life phenomena.
results primarily simulation-based. Rigorous mathematical results are only coming out.