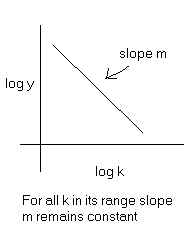Discussion Notes
Feb 23, 2001 (courtesy Ali A Zafer)
Diameter of the Web
Authors estimation leads to 19 links, assuming power-law
connectivities. Fernando raised important points about extrapolation
from nd.edu results.
In a future class, we will see quite different estimates, based on more
detailed mappings of the web.
Classes of Behavior of Small-World Networks
Last class, we pointed out discrepancies between degree distributions
posited by the WS model and observed degree distributions of graphs.
This paper characterizes these distributions more closely.
- Scale-free networks: vertex connectivities follow strictly
a power law:
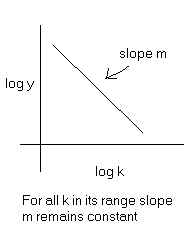
Two reasons are put forth to explain power-law behavior: (i)
growth, and (ii) preferential attachment (the rich get richer).
- Broad-scale networks:
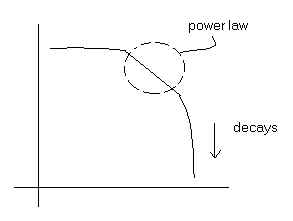
There is a distinct power-law region, followed by a steep tail.
The authors indicate that reasons could be aging and capacity
constraints, which cause a deviation from a power-law. In the instructor's experience, another cause has
been brought to attention in the movies domain: expectation.
Some movies start off with a low expectation and then acquire
edges (e.g., "The Sixth Sense"). Sometimes movies start off with
a high expectation and we can witness a drop in the rate at
which they acquire edges (e.g., "The Phantom Menace"). These
can also cause deviations from power-law behavior.
- Single-scale networks: Has a fast decaying tail, such as a
Poisson or Gaussian.
The WS model (discussed previous class) does not address issues of
growth, preferential attachment, and the power-law behavior seen
by most graphs. Power-laws, having been cited in so many places,
are now believed to be influential in characterizing
robustness & fragility of natural
and artificial systems (John Doyle's slides).
|