Module of non-intrinsic mathematical operations. Contains all the operations necessary for multi body dynamics computations not supported by the Fortran 2003 standard. More...
Functions/Subroutines | |
| REAL(8) | norm (r) |
Calculate the standard 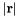 of a vector of a vector 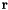 . . | |
| REAL(8), dimension(size(r)) | normalize (r) |
Normalize an vector 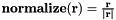 . . | |
| REAL(8), dimension(3) | pvect (u, v) |
| Calculates the cross product of two vectors. | |
| subroutine | PerpVectors (nfl, u, v) |
| Given a vector, calculates two perpendicular vectors to the given one. | |
| real(8) | MREulerParam (e) |
Given the vector of Euler parameters 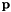 , it returns the rotation transformation matrix , it returns the rotation transformation matrix 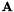 . . | |
| real(8) | Atp_v (p, v) |
Given the vector of Euler parameters 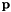 , it returns the matrix , it returns the matrix 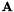 . . | |
| real(8) | Gmatrix (e) |
Given the vector of Euler parameters  , it returns the G matrix , it returns the G matrix 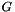 . . | |
| real(8) | Gtp_v (v) |
Given the vector of Euler parameters 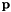 and a vector and a vector 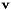 , it returns the , it returns the 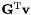 matrix. matrix. | |
| real(8) | dMREulerParam_v (e, v) |
Given the vector of Euler parameters  and a vecter and a vecter 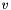 , it returns , it returns 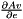 . . | |
| real(8) | dMREulerParam_t (p, pd, t) |
Given the vector of Euler parameters  , the velocity vector of Euler parameters , the velocity vector of Euler parameters 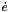 and a vector and a vector 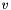 , it returns , it returns 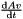 . . | |
| real(8) | d2MREulerParam_t2 (p, pd, ps, t) |
Given the vector of Euler parameters  , the velocity vector of Euler parameters , the velocity vector of Euler parameters 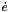 and a vector and a vector 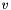 , it returns , it returns 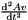 . . | |
| real(8) | dMREulerParam_t_e1 (p, pd, t) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 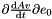 . . | |
| real(8) | dMREulerParam_t_e2 (p, pd, t) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 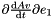 . . | |
| real(8) | dMREulerParam_t_e3 (p, pd, t) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 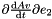 . . | |
| real(8) | dMREulerParam_t_e4 (p, pd, t) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 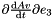 . . | |
| real(8) | dMREulerParam_t_e1d (p, pd, t) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 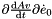 . . | |
| real(8) | dMREulerParam_t_e2d (p, pd, t) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 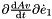 . . | |
| real(8) | dMREulerParam_t_e3d (p, pd, t) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 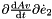 . . | |
| real(8) | dMREulerParam_t_e4d (p, pd, t) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 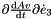 . . | |
| real(8) | dMREulerParam_v_e1 (e, v) |
Given the vector of Euler parameters  and a vecter and a vecter 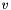 , it returns , it returns 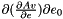 . . | |
| real(8) | dMREulerParam_v_e2 (e, v) |
Given the vector of Euler parameters  and a vecter and a vecter 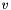 , it returns , it returns 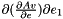 . . | |
| real(8) | dMREulerParam_v_e3 (e, v) |
Given the vector of Euler parameters  and a vecter and a vecter 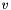 , it returns , it returns 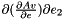 . . | |
| real(8) | dMREulerParam_v_e4 (e, v) |
Given the vector of Euler parameters  and a vecter and a vecter 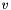 , it returns , it returns 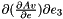 . . | |
| real(8) | MREulerParam_e1 (e) |
Given the vector of Euler parameters  , it returns the derivative of the rotation matrix with respect to , it returns the derivative of the rotation matrix with respect to 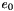 . . | |
| real(8) | MREulerParam_e2 (e) |
Given the vector of Euler parameters  , it returns the derivative of the rotation matrix with respect to , it returns the derivative of the rotation matrix with respect to 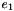 . . | |
| real(8) | MREulerParam_e3 (e) |
Given the vector of Euler parameters  , it returns the derivative of the rotation matrix with respect to , it returns the derivative of the rotation matrix with respect to 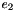 . . | |
| real(8) | MREulerParam_e4 (e) |
Given the vector of Euler parameters  , it returns the derivative of the rotation matrix with respect to , it returns the derivative of the rotation matrix with respect to 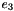 . . | |
| real(8), dimension(size(u), size(v)) | tensor_product (u, v) |
| Given the two vectors, find the tensor product between these two vectors. | |
| real(8), dimension(3, 3) | skew (a) |
| Given one vector, find the skew symmetric matrix for this vector. | |
Variables | |
| REAL(8), dimension(3, 3), parameter | EYE3 = RESHAPE(SOURCE=(/ 1.d0,0.d0,0.d0, 0.d0,1.d0,0.d0, 0.d0,0.d0,1.d0/), SHAPE=(/3,3/)) |
| REAL(8), dimension(3, 3), parameter | ZEROS3 = 0.d0 |
| REAL(8), dimension(4, 4), parameter | EYE4 = RESHAPE(SOURCE=(/ 1.d0,0.d0,0.d0,0.d0, 0.d0,1.d0,0.d0,0.d0, 0.d0,0.d0,1.d0,0.d0, 0.d0,0.d0,0.d0,1.d0/), SHAPE=(/4,4/)) |
| REAL(8), dimension(3, 4), parameter | Gmatrix_p1 = reshape([0.d0, 0.d0, 0.d0, 1.d0, 0.d0, 0.d0, 0.d0, 1.d0, 0.d0, 0.d0, 0.d0, 1.d0], [3, 4]) |
| REAL(8), dimension(3, 4), parameter | Gmatrix_p2 = reshape([-1.d0, 0.d0, 0.d0, 0.d0, 0.d0, 0.d0, 0.d0, 0.d0, -1.d0, 0.d0, 1.d0, 0.d0], [3, 4]) |
| REAL(8), dimension(3, 4), parameter | Gmatrix_p3 = reshape([0.d0, -1.d0, 0.d0, 0.d0, 0.d0, 1.d0, 0.d0, 0.d0, 0.d0, -1.d0, 0.d0, 0.d0], [3, 4]) |
| REAL(8), dimension(3, 4), parameter | Gmatrix_p4 = reshape([0.d0, 0.d0, -1.d0, 0.d0, -1.d0, 0.d0, 1.d0, 0.d0, 0.d0, 0.d0, 0.d0, 0.d0], [3, 4]) |
Detailed Description
Module of non-intrinsic mathematical operations. Contains all the operations necessary for multi body dynamics computations not supported by the Fortran 2003 standard.
Function/Subroutine Documentation
| real(8) math_oper::Atp_v | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(3),intent(in) | v | ||
| ) |
Given the vector of Euler parameters 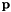 , it returns the matrix
, it returns the matrix 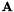 .
.
- Parameters:
-
e vector of Euler parameters.
| real(8) math_oper::d2MREulerParam_t2 | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(4),intent(in) | ps, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters  , the velocity vector of Euler parameters
, the velocity vector of Euler parameters 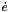 and a vector
and a vector 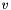 , it returns
, it returns 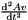 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the first derivative of Euler parameters. ps vector of the second derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_t | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters  , the velocity vector of Euler parameters
, the velocity vector of Euler parameters 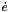 and a vector
and a vector 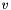 , it returns
, it returns 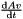 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_t_e1 | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 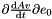 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_t_e1d | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 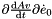 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_t_e2 | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 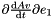 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_t_e2d | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 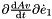 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_t_e3 | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 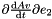 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_t_e3d | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 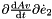 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_t_e4 | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 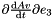 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_t_e4d | ( | real(8),dimension(4),intent(in) | p, |
| real(8),dimension(4),intent(in) | pd, | ||
| real(8),dimension(3),intent(in) | t | ||
| ) |
Given the vector of Euler parameters, the velocity vector of Euler parameters and a vector, it returns 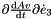 .
.
- Parameters:
-
p vector of Euler parameters. pd vector of the derivative of Euler parameters. t vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_v | ( | real(8),dimension(4),intent(in) | e, |
| real(8),dimension(3),intent(in) | v | ||
| ) |
Given the vector of Euler parameters  and a vecter
and a vecter 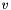 , it returns
, it returns 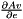 .
.
- Parameters:
-
e vector of Euler parameters. v vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_v_e1 | ( | real(8),dimension(4),intent(in) | e, |
| real(8),dimension(3),intent(in) | v | ||
| ) |
Given the vector of Euler parameters  and a vecter
and a vecter 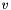 , it returns
, it returns 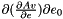 .
.
- Parameters:
-
e vector of Euler parameters. v vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_v_e2 | ( | real(8),dimension(4),intent(in) | e, |
| real(8),dimension(3),intent(in) | v | ||
| ) |
Given the vector of Euler parameters  and a vecter
and a vecter 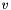 , it returns
, it returns 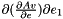 .
.
- Parameters:
-
e vector of Euler parameters. v vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_v_e3 | ( | real(8),dimension(4),intent(in) | e, |
| real(8),dimension(3),intent(in) | v | ||
| ) |
Given the vector of Euler parameters  and a vecter
and a vecter 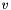 , it returns
, it returns 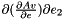 .
.
- Parameters:
-
e vector of Euler parameters. v vector given in the body reference frame.
| real(8) math_oper::dMREulerParam_v_e4 | ( | real(8),dimension(4),intent(in) | e, |
| real(8),dimension(3),intent(in) | v | ||
| ) |
Given the vector of Euler parameters  and a vecter
and a vecter 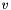 , it returns
, it returns 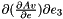 .
.
- Parameters:
-
e vector of Euler parameters. v vector given in the body reference frame.
| real(8) math_oper::Gmatrix | ( | real(8),dimension(4),intent(in) | e | ) |
Given the vector of Euler parameters  , it returns the G matrix
, it returns the G matrix 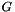 .
.
- Parameters:
-
e vector of Euler parameters.
| real(8) math_oper::Gtp_v | ( | real(8),dimension(3),intent(in) | v | ) |
Given the vector of Euler parameters 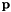 and a vector
and a vector 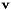 , it returns the
, it returns the 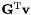 matrix.
matrix.
- Parameters:
-
p vector of Euler parameters.
| real(8) math_oper::MREulerParam | ( | real(8),dimension(4),intent(in) | e | ) |
Given the vector of Euler parameters 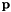 , it returns the rotation transformation matrix
, it returns the rotation transformation matrix 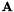 .
.
- Parameters:
-
p vector of Euler parameters.
| real(8) math_oper::MREulerParam_e1 | ( | real(8),dimension(4),intent(in) | e | ) |
Given the vector of Euler parameters  , it returns the derivative of the rotation matrix with respect to
, it returns the derivative of the rotation matrix with respect to 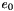 .
.
- Parameters:
-
e vector of Euler parameters.
| real(8) math_oper::MREulerParam_e2 | ( | real(8),dimension(4),intent(in) | e | ) |
Given the vector of Euler parameters  , it returns the derivative of the rotation matrix with respect to
, it returns the derivative of the rotation matrix with respect to 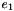 .
.
- Parameters:
-
e vector of Euler parameters.
| real(8) math_oper::MREulerParam_e3 | ( | real(8),dimension(4),intent(in) | e | ) |
Given the vector of Euler parameters  , it returns the derivative of the rotation matrix with respect to
, it returns the derivative of the rotation matrix with respect to 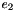 .
.
- Parameters:
-
e vector of Euler parameters.
| real(8) math_oper::MREulerParam_e4 | ( | real(8),dimension(4),intent(in) | e | ) |
Given the vector of Euler parameters  , it returns the derivative of the rotation matrix with respect to
, it returns the derivative of the rotation matrix with respect to 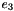 .
.
- Parameters:
-
e vector of Euler parameters.
| REAL(8) math_oper::norm | ( | REAL(8),dimension(:) | r | ) |
Calculate the standard 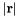 of a vector
of a vector 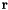 .
.
- Parameters:
-
r vector.
| REAL(8),dimension(size(r)) math_oper::normalize | ( | REAL(8),dimension(:) | r | ) |
Normalize an vector 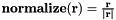 .
.
- Parameters:
-
r vector
| subroutine math_oper::PerpVectors | ( | REAL(8),dimension(3),intent(in) | nfl, |
| REAL(8),dimension(3),intent(out) | u, | ||
| REAL(8),dimension(3),intent(out) | v | ||
| ) |
Given a vector, calculates two perpendicular vectors to the given one.
- Parameters:
-
nfl given vector.

| REAL(8),dimension(3) math_oper::pvect | ( | REAL(8),dimension(:),intent(in) | u, |
| REAL(8),dimension(:),intent(in) | v | ||
| ) |
Calculates the cross product of two vectors.
- Parameters:
-
u,v vectors involved.
| real(8),dimension(3,3) math_oper::skew | ( | real(8),dimension(3),intent(in) | a | ) |
Given one vector, find the skew symmetric matrix for this vector.
- Parameters:
-
a the input vector
| real(8),dimension(size(u),size(v)) math_oper::tensor_product | ( | real(8),dimension(:) | u, |
| real(8),dimension(:) | v | ||
| ) |
Given the two vectors, find the tensor product between these two vectors.
- Parameters:
-
u the first vector v the second vector
Variable Documentation
| REAL(8),dimension(3,3),parameter math_oper::EYE3 = RESHAPE(SOURCE=(/ 1.d0,0.d0,0.d0, 0.d0,1.d0,0.d0, 0.d0,0.d0,1.d0/), SHAPE=(/3,3/)) |
| REAL(8),dimension(4,4),parameter math_oper::EYE4 = RESHAPE(SOURCE=(/ 1.d0,0.d0,0.d0,0.d0, 0.d0,1.d0,0.d0,0.d0, 0.d0,0.d0,1.d0,0.d0, 0.d0,0.d0,0.d0,1.d0/), SHAPE=(/4,4/)) |
| REAL(8),dimension(3,4),parameter math_oper::Gmatrix_p1 = reshape([0.d0, 0.d0, 0.d0, 1.d0, 0.d0, 0.d0, 0.d0, 1.d0, 0.d0, 0.d0, 0.d0, 1.d0], [3, 4]) |
| REAL(8),dimension(3,4),parameter math_oper::Gmatrix_p2 = reshape([-1.d0, 0.d0, 0.d0, 0.d0, 0.d0, 0.d0, 0.d0, 0.d0, -1.d0, 0.d0, 1.d0, 0.d0], [3, 4]) |
| REAL(8),dimension(3,4),parameter math_oper::Gmatrix_p3 = reshape([0.d0, -1.d0, 0.d0, 0.d0, 0.d0, 1.d0, 0.d0, 0.d0, 0.d0, -1.d0, 0.d0, 0.d0], [3, 4]) |
| REAL(8),dimension(3,4),parameter math_oper::Gmatrix_p4 = reshape([0.d0, 0.d0, -1.d0, 0.d0, -1.d0, 0.d0, 1.d0, 0.d0, 0.d0, 0.d0, 0.d0, 0.d0], [3, 4]) |
| REAL(8),dimension(3,3),parameter math_oper::ZEROS3 = 0.d0 |
 1.7.4
1.7.4