Module of primitive constraints. It's NOT a user module, it's used by the solver. More...
Functions/Subroutines | |
| subroutine | restric_Setup |
| subroutine | deallocfi |
| subroutine | r_UnitEulParam (ir, iEul) |
Primitive constraint of unitary Euler parameters assume 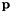 is the Euler parameter.the constraint equation is : is the Euler parameter.the constraint equation is : 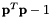 . . | |
| subroutine | r_dot1GB (ir, iEul2, u, v) |
| Primitive dot-1 constraint of a body attached on the ground. | |
| subroutine | r_dot1 (ir, iEul1, iEul2, u, v) |
Primitive dot-1 constraint assume 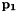 and and 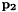 are the Euler parameter of body 1 and body 2 and are the Euler parameter of body 1 and body 2 and 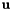 and and 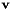 are two vectors attached on body 1 and body 2 in the body reference frame, the constraint equation is : are two vectors attached on body 1 and body 2 in the body reference frame, the constraint equation is : 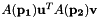 . . | |
| subroutine | r_sphericalGB (ir, irg2, iEul2, pt1, pt2) |
Primitive constraints of a spherical joint of a body attached to the ground The three constraint equations are : 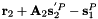 . . | |
| subroutine | r_spherical (ir, irg1, irg2, iEul1, iEul2, pt1, pt2) |
Primitive constraints of a spherical joint between two bodies The three constraint equations are : 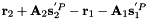 . . | |
| subroutine | r_revoluteGB (ir, irg2, iEul2, pt1, pt2, u1, v1, vec2) |
Primitive constraints of a revolute joint of a body attached to the ground The first three constraint equations are : 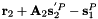 The fouth constraint equation is: The fouth constraint equation is: 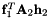 The fifth constraint equation is: The fifth constraint equation is: 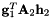 . . | |
| subroutine | r_revolute (ir, irg1, irg2, iEul1, iEul2, pt1, pt2, u1, v1, vec2) |
Primitive constraints of a revolute joint between two bodies The three constraint equations are : 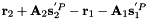 The fouth constraint equation is: The fouth constraint equation is: 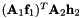 The fifth constraint equation is: The fifth constraint equation is: 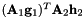 . . | |
| subroutine | r_transGB (ir, irg2, iEul2, pt1, pt2, vec1y, vec1x, vec2x, vec2z) |
Primitive constraints of a translational joint of a body attached to the ground The first constraint equation is: 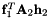 The second constraint equation is: The second constraint equation is: 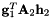 The third constraint equation is: The third constraint equation is: 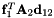 The forth constraint equation is: The forth constraint equation is: 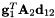 The fifth constraint equation is: The fifth constraint equation is: 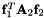 . . | |
| subroutine | r_trans (ir, irg1, irg2, iEul1, iEul2, pt1, pt2, vec1y, vec1x, vec2x, vec2z) |
Primitive constraints of a translational joint between two bodies. The first constraint equation is: 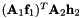 The second constraint equation is: The second constraint equation is: 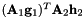 The third constraint equation is: The third constraint equation is: 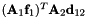 The forth constraint equation is: The forth constraint equation is: 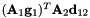 The fifth constraint equation is: The fifth constraint equation is: 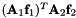 . . | |
| subroutine | r_Drive_rgEul (ir, ind, i_MOTOR) |
| Primitive driving constraints for a generalized coordinate of the system. | |
| subroutine | r_Drive_distGB (ir, irg2, iEul2, pt1, pt2_loc, i_MOTOR) |
| Primitive driving constraints for a distance between a point in the ground and a point of one body. | |
| subroutine | r_Drive_dist (ir, irg1, irg2, iEul1, iEul2, pt1_loc, pt2_loc, i_MOTOR) |
| Primitive driving constraints for a distance between two points of two bodies. | |
Variables | |
| REAL(8), dimension(:), allocatable | PROTECTED |
| REAL(8), dimension(:), allocatable | fi |
Detailed Description
Module of primitive constraints. It's NOT a user module, it's used by the solver.
Function/Subroutine Documentation
| subroutine restric::deallocfi | ( | ) |
| subroutine restric::r_dot1 | ( | integer,intent(in) | ir, |
| integer,dimension(4),intent(in) | iEul1, | ||
| integer,dimension(4),intent(in) | iEul2, | ||
| real(8),dimension(3),intent(in) | u, | ||
| real(8),dimension(3),intent(in) | v | ||
| ) |
Primitive dot-1 constraint assume 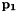 and
and 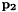 are the Euler parameter of body 1 and body 2 and
are the Euler parameter of body 1 and body 2 and 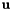 and
and 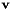 are two vectors attached on body 1 and body 2 in the body reference frame, the constraint equation is :
are two vectors attached on body 1 and body 2 in the body reference frame, the constraint equation is : 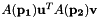 .
.
- Parameters:
-
ir index of the constraint iEul1,iEul2 indexes of the Euler parameters of the bodies. u vector in the first body given in the body reference frame v vector in the second body given in the body reference frame

| subroutine restric::r_dot1GB | ( | integer,intent(in) | ir, |
| integer,dimension(4),intent(in) | iEul2, | ||
| real(8),dimension(3),intent(in) | u, | ||
| real(8),dimension(3),intent(in) | v | ||
| ) |
Primitive dot-1 constraint of a body attached on the ground.
- Parameters:
-
ir index of the constraint iEul2 indexes of the Euler parameters of the body. u vector attached on the ground v vector in the second body given in the body reference frame assume  are the Euler parameter of the body the constraint equation is :
are the Euler parameter of the body the constraint equation is : 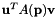

| subroutine restric::r_Drive_dist | ( | INTEGER,intent(in) | ir, |
| INTEGER,dimension(3),intent(in) | irg1, | ||
| INTEGER,dimension(3),intent(in) | irg2, | ||
| INTEGER,dimension(4),intent(in) | iEul1, | ||
| INTEGER,dimension(4),intent(in) | iEul2, | ||
| REAL(8),dimension(3),intent(in) | pt1_loc, | ||
| REAL(8),dimension(3),intent(in) | pt2_loc, | ||
| INTEGER,intent(in) | i_MOTOR | ||
| ) |
Primitive driving constraints for a distance between two points of two bodies.
- Parameters:
-
ir index of the constraint. irg1,irg2 index of the center of mass of the body. iEul1,iEul2 index of the Euler parameters of the body. pt1_loc,pt2_loc points in the bodies given in the bodies reference frames. i_MOTOR index in the vector of motors (STATE::pos) to drive the constraint.

| subroutine restric::r_Drive_distGB | ( | INTEGER,intent(in) | ir, |
| INTEGER,dimension(3),intent(in) | irg2, | ||
| INTEGER,dimension(4),intent(in) | iEul2, | ||
| REAL(8),dimension(3),intent(in) | pt1, | ||
| REAL(8),dimension(3),intent(in) | pt2_loc, | ||
| INTEGER,intent(in) | i_MOTOR | ||
| ) |
Primitive driving constraints for a distance between a point in the ground and a point of one body.
- Parameters:
-
ir index of the constraint. irg2 index of the center of mass of the body. iEul2 index of the Euler parameters of the body. pt1 point in the ground given in the global reference frame pt2_loc point in the second body given in the body reference frame i_MOTOR index in the vector of motors (STATE::pos) to drive the constraint.

| subroutine restric::r_Drive_rgEul | ( | INTEGER,intent(in) | ir, |
| INTEGER,intent(in) | ind, | ||
| INTEGER,intent(in) | i_MOTOR | ||
| ) |
Primitive driving constraints for a generalized coordinate of the system.
- Parameters:
-
ir index of the constraint ind index of the driven generalized coordinate. i_MOTOR index in the vector of motors (STATE::pos) to drive the constraint.
| subroutine restric::r_revolute | ( | integer,intent(in) | ir, |
| integer,dimension(3),intent(in) | irg1, | ||
| integer,dimension(3),intent(in) | irg2, | ||
| integer,dimension(4),intent(in) | iEul1, | ||
| integer,dimension(4),intent(in) | iEul2, | ||
| REAL(8),dimension(3),intent(in) | pt1, | ||
| REAL(8),dimension(3),intent(in) | pt2, | ||
| REAL(8),dimension(3),intent(in) | u1, | ||
| REAL(8),dimension(3),intent(in) | v1, | ||
| REAL(8),dimension(3),intent(in) | vec2 | ||
| ) |
Primitive constraints of a revolute joint between two bodies The three constraint equations are : 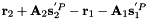 The fouth constraint equation is:
The fouth constraint equation is: 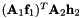 The fifth constraint equation is:
The fifth constraint equation is: 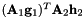 .
.
- Parameters:
-
ir index of the constraint irg1,irg2 indexes of the centers of mass of the bodies. iEul1,iEul2 indexes of the Euler parameters of the bodies. pt1 point in the first body given in the body reference frame pt2 point in the second body given in the body reference frame u1,v1 perpendicular vectors in the first body given in the body reference frame vec2 vector in the second body given in the body reference frame

| subroutine restric::r_revoluteGB | ( | integer,intent(in) | ir, |
| integer,dimension(3),intent(in) | irg2, | ||
| integer,dimension(4),intent(in) | iEul2, | ||
| REAL(8),dimension(3),intent(in) | pt1, | ||
| REAL(8),dimension(3),intent(in) | pt2, | ||
| REAL(8),dimension(3),intent(in) | u1, | ||
| REAL(8),dimension(3),intent(in) | v1, | ||
| REAL(8),dimension(3),intent(in) | vec2 | ||
| ) |
Primitive constraints of a revolute joint of a body attached to the ground The first three constraint equations are : 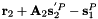 The fouth constraint equation is:
The fouth constraint equation is: 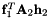 The fifth constraint equation is:
The fifth constraint equation is: 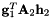 .
.
- Parameters:
-
ir index of the constraint irg2 index of the center of mass of the body iEul2 index of the Euler parameters of the body pt1 point in the ground pt2 point in the body given in the body reference frame u1,v1 perpendicular vectors in the ground vec2 vector in the body given in the body reference frame

| subroutine restric::r_spherical | ( | integer,intent(in) | ir, |
| integer,dimension(3),intent(in) | irg1, | ||
| integer,dimension(3),intent(in) | irg2, | ||
| integer,dimension(4),intent(in) | iEul1, | ||
| integer,dimension(4),intent(in) | iEul2, | ||
| real(8),dimension(3),intent(in) | pt1, | ||
| real(8),dimension(3),intent(in) | pt2 | ||
| ) |
Primitive constraints of a spherical joint between two bodies The three constraint equations are : 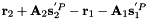 .
.
- Parameters:
-
ir index of the constraint irg1,irg2 indexes of the centers of mass of the bodies. iEul1,iEul2 indexes of the Euler parameters of the bodies. pt1 point in the first body given in the body reference frame pt2 point in the second body given in the body reference frame

| subroutine restric::r_sphericalGB | ( | integer,intent(in) | ir, |
| integer,dimension(3),intent(in) | irg2, | ||
| integer,dimension(4),intent(in) | iEul2, | ||
| real(8),dimension(3),intent(in) | pt1, | ||
| real(8),dimension(3),intent(in) | pt2 | ||
| ) |
Primitive constraints of a spherical joint of a body attached to the ground The three constraint equations are : 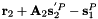 .
.
- Parameters:
-
ir index of the constraint irg2 index of the center of mass of the body iEul2 index of the Euler parameters of the body pt1 point in the ground pt2 point in the body given in the body reference frame

| subroutine restric::r_trans | ( | integer,intent(in) | ir, |
| integer,dimension(3),intent(in) | irg1, | ||
| integer,dimension(3),intent(in) | irg2, | ||
| integer,dimension(4),intent(in) | iEul1, | ||
| integer,dimension(4),intent(in) | iEul2, | ||
| REAL(8),dimension(3),intent(in) | pt1, | ||
| REAL(8),dimension(3),intent(in) | pt2, | ||
| REAL(8),dimension(3),intent(in) | vec1y, | ||
| REAL(8),dimension(3),intent(in) | vec1x, | ||
| REAL(8),dimension(3),intent(in) | vec2x, | ||
| REAL(8),dimension(3),intent(in) | vec2z | ||
| ) |
Primitive constraints of a translational joint between two bodies. The first constraint equation is: 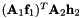 The second constraint equation is:
The second constraint equation is: 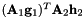 The third constraint equation is:
The third constraint equation is: 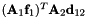 The forth constraint equation is:
The forth constraint equation is: 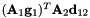 The fifth constraint equation is:
The fifth constraint equation is: 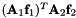 .
.
- Parameters:
-
ir index of the constraint irg1,irg2 indexes of the centers of mass of the bodies. iEul1,iEul2 indexes of the Euler parameters of the bodies. pt1 point given in the first body given in the body reference frame pt2 point given in the second body given in the body reference frame vec1y,vec1x perpendicular vectors in the first body given in the body reference frame vec2x,vec2z perpendicular vectors in the second body given in the body reference frame

| subroutine restric::r_transGB | ( | integer,intent(in) | ir, |
| integer,dimension(3),intent(in) | irg2, | ||
| integer,dimension(4),intent(in) | iEul2, | ||
| REAL(8),dimension(3),intent(in) | pt1, | ||
| REAL(8),dimension(3),intent(in) | pt2, | ||
| REAL(8),dimension(3),intent(in) | vec1y, | ||
| REAL(8),dimension(3),intent(in) | vec1x, | ||
| REAL(8),dimension(3),intent(in) | vec2x, | ||
| REAL(8),dimension(3),intent(in) | vec2z | ||
| ) |
Primitive constraints of a translational joint of a body attached to the ground The first constraint equation is: 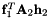 The second constraint equation is:
The second constraint equation is: 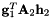 The third constraint equation is:
The third constraint equation is: 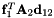 The forth constraint equation is:
The forth constraint equation is: 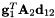 The fifth constraint equation is:
The fifth constraint equation is: 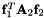 .
.
- Parameters:
-
ir index of the constraint irg2 index of the center of mass of the body iEul2 index of the Euler parameter of the body. pt1 point in the ground pt2 point in the body given in the body reference frame vec1y,vec1x perpendicular vectors in the ground vec2x,vec2z perpendicular vectors in the body given in the body reference frame

| subroutine restric::r_UnitEulParam | ( | integer,intent(in) | ir, |
| integer,dimension(4),intent(in) | iEul | ||
| ) |
Primitive constraint of unitary Euler parameters assume 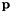 is the Euler parameter.the constraint equation is :
is the Euler parameter.the constraint equation is : 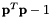 .
.
- Parameters:
-
ir index of the constraint iEul indexes of the Euler parameters
| subroutine restric::restric_Setup | ( | ) |

Variable Documentation
| REAL(8),dimension(:),allocatable restric::fi |
| REAL(8),dimension(:),allocatable restric::PROTECTED |
 1.7.4
1.7.4