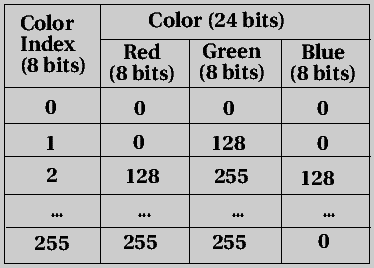
- The midpoint scan conversion algorithm covered in class (below)
is applicable only for lines having slopes between zero and 1. Modify
this algorithm to accomodate lines having slopes between 1 and
infinity (lines with angles between 45 degrees and vertical).
Short derivation. The decision to be made is between N and NE.
The midpoint to be tested is at (xp+0.5, yp+1):
| Quantity |
Variable |
Expression |
Value |
| Decision variable |
dp |
F(xp+0.5, yp+1) |
a(xp+0.5) + b(yp+1) + c |
| Initial value |
d0 |
F(x0+0.5,y0+1) |
a/2 + b |
| N chosen |
dp+1 |
F(xp+0.5,yp+2) |
a(xp+0.5) + b(yp+2) + c |
| - |
incrN |
- |
b (= -dx) |
| NE chosen |
dp+1 |
F(xp+1.5,yp+2) |
a(xp+1.5) + b(yp+2) + c |
| - |
incrNE |
- |
a+b (= dy-dx) |
Here is code for lines with slopes between 1 and infinity:
void MidpointLine (int x0, int y0, int x1, int y1, int value)
{
int dx = x1 - x0;
int dy = y1 - y0;
int d = dy - 2 * dx; /* initial value of d */
int incrN = -2 * dx; /* incr used for move to N */
int incrNE = 2 * (dy - dx); /* incr used for move to NE */
int x = x0;
int y = y0;
WritePixel (x, y, value); /* the start pixel */
while (y < y1) {
if (d <= 0) { /* choose NE */
d += incrNE;
x++;
y++;
} else { /* choose N */
d += incrN;
y++;
}
WritePixel (x, y, value); /* the selected pixel */
}
}
- Suppose you want to scan convert a curve expressed by the
equation a + bx + cx2 + y = 0. For
this question, consider only the case where you are currently in a
region on the curve where the local slope is between 0 and 1...
(A)Suppose you are at point (xp, yp) on
the scan converted curve. Use the procedure described in class and in
the text to derive the expression for decision variable d, which will
be used to determine the next pixel to be highlighted.
- d = F(xp+1, yp+0.5) = a +
b(xp + 1) + c(xp + 1)2 + (yp+0.5)
(B)If d > 0, which pixel (E or NE) is highlighted next?
An increase in y will increase d. Based on this test, d > 0
implies that the midpoint is above the line (the line passes below the
midpoint), and so we should choose E.
(C)An iterative algorithm can be used to increment the value of
the decision variable at each step. Let d' be the decision variable
for the point following (xp, yp). Define deltaE
as (d'-d) when pixel E is chosen next and deltaNE as (d'-d) when pixel
NE is chosen next. Write expressions for deltaE and deltaNE as
functions of a, b, c, xp, and yp.
-
| deltaE
| = (d'-d)E
| = [F(xp+2, yp+0.5) - F(xp+1,
yp+0.5)]
| = b + c(2xp + 3)
|
| deltaNE
| = (d'-d)NE
| = [F(xp+2, yp+1.5) - F(xp+1,
yp+0.5)]
| = b + c(2xp + 3) + 1
|
(D)Although the first order differences deltaE and deltaNE
depend on xp, the second order differences depend only on
coefficients a, b, and c. Let d'' be the decision parameter for the
second point following (xp, yp). The second
order difference is defined as [(d''-d') - (d'-d)]. Find the changes in deltaE
and deltaNE when E or NE is chosen as the second point (4 cases in
total). Hint: this is very similar to the midpoint circle algorithm
in Section 3.3.2.
E chosen: next pixel is (xp+1, yp)
-
| (deltaEnew - deltaE)
| = [b + c(2(xp+1) + 3)] - [b + c(2xp + 3)]
| = 2c
|
| (deltaNEnew - deltaNE)
| = [b + c(2(xp+1) + 3) + 1] - [b + c(2xp +
3) + 1]
| = 2c
|
NE chosen: next pixel is (xp+1, yp+1)
-
| (deltaEnew - deltaE)
| = [b + c(2(xp+1) + 3)] - [b + c(2xp + 3)]
| = 2c
|
| (deltaNEnew - deltaNE)
| = [b + c(2(xp+1) + 3) + 1] - [b + c(2xp +
3) + 1]
| = 2c
|
- Rapid scan conversion of scenes is a bottleneck to creating
complex animations in real-time. To speed this process, some research
(e.g., the Pixel Planes
project at the University of North Carolina) has focused on
constructing parallel hardware for computer graphics. One idea is
that an image can have a single processor for every pixel. Then, to
display a line on the screen, a graphics package could broadcast the
equation for the line, and the processor representing each pixel could
decide what its intensity value should be.
Assume that we have only two intensity values: on and off, and our
application wants to draw a line of width w. The equation for the
line is ax + by + c = 0. Each processor knows its x and y location.
Coefficients a, b, and c are broadcast to all processors.
(A) Describe (in words) a simple algorithm that a processor
can use to determine whether the pixel it represents should be on or
off. Do not worry about clipping the line at its endpoints. One
solution would be for each processor to compute its distance from the
ideal (zero width) line, and to highlight itself if and only if this
distance is less than w/2.
(B) Derive an expression as a function of w, a, b, c, x, and y
that must be true for the pixel at (x,y) to be turned on. You may
want to use the expression for distance to the line: [(ax + by + c) /
sqrt(a2 + b2)]
-
[(ax + by + c) / sqrt(a2 + b2)] < w/2
(C) Computations performed on the main computer are usually
much faster than computations performed on individual processors. It
it is also expensive to broadcast information to the processors. What
computations could you do on the main computer that would reduce the
amount of information transferred and reduce amount of work each
processor has to do?
If the speed difference is very large, reformulate the inequality
as:
- ax + by < [w/2 * sqrt(a2 + b2) -
c]
Let g = [w/2 * sqrt(a2 + b2) - c] be computed on
the main processor and broadcast a,b, and g.
If the speed difference is not as great, and we wish to avoid
fractional arithmetic and the sqrt operation, it might be better to
reformulate the inequality as:
- 4(ax + by + c)2 < w2 (a2
+ b2)
Let g = w2 (a2 + b2) be computed on
the main processor and broadcast a, b, c, and g.
- Suppose we are filling a circle with a pattern and want the
circle to look the same regardless of its position in the window
(xc, yc). Given an MxN pattern array
P[M][N] and function WritePixel(x, y, color), write a
code fragment to select the pattern element to be displayed at point
(x, y) inside the circle.
/* get circle-registered, positive x value */
px = x - xc;
while (px < 0)
px += M;
/* get circle-registered, positive y value */
py = y - yc;
while (py < 0)
py += N;
/* write appropriate pattern element
(assume P is an array of color values */
WritePixel(x, y, P[px%M][py%N]);
- Modify the midpoint algorithm to display a dashed line with
thickness of 4 pixels. Discuss the pros and cons of the approach you
chose.
To get a thick line, one option is to use the "replicated pixels"
technique. For lines with |slope| <= 1, the midpointLine algorithm
iterates over columns. This means that for each column, the extra
pixels should be stacked above and below the pixel selected by the
midpointLine algorithm. To incorporate the replicating pixels
technique into the midpointLine algorithm for lines where |slope| <=
1, replace the following call:
WritePixel (x, y, value); /* the selected pixel */
with this code, where the lineMask pattern is used to make the line
appear dashed:
int lineMask[8] = {0,0,0,0,1,1,1,1};
if (lineMask[x % 8]) {
WritePixel(x, y, value);
WritePixel(x, y+1, value);
WritePixel(x, y+2, value);
WritePixel(x, y-1, value);
}
For lines with |slope| > 1, the midpointLine algorithm iterates
over rows, so pixels are duplicated in rows. The corresponding code
is:
if (lineMask[x % 8]) {
WritePixel(x, y, value);
WritePixel(x+1, y, value);
WritePixel(x+2, y, value);
WritePixel(x-1, y, value);
}
Pros: Both the use of the line mask and the technique of
replicating pixels are very fast.
Cons:
- Gaps. Suppose we have two lines, one where columns are replicated
and one where rows are replicated. If these two lines meet at a vertex,
there will be a gap in the thick line at that vertex.
- The line is off-center for even-valued thicknesses. In the
example above, two pixels are filled in on top of or to the right of
the pixel selected by the midpointLine algorithm, but only one pixel
is filled in on the bottom or left.
- Intensity varies with angle. This is due to the fact that the
number of pixels highlighted for a line depends only on the number of
rows or columns spanned by that line, regardless of line angle or line
length. For example, a line of fixed length will span a varying
number of rows or columns depending on its angle. This will cause its
intensity to vary by angle.
- Dashed lines will have dashes of different lengths at different
line angles. This is due to the fact that the dashes are turned on
and off based on the number of columns or rows traversed by the
midpointLine algorithm, instead of based on the length of the line.
Dashes will be shortest for horizontal or vertical lines, longest at
45 degrees from horizontal or vertical.
- Dash edges will not be aligned with the line. Each dash will
appear to have two edges that are either horizontal or vertical
instead of being aligned with the line that is being drawn. This
effect will be especially disturbing for thick dashes in a line at a
45 degree angle.
- The Gupta-Sproull anti-aliasing algorithm does weighted area
sampling using a cone filter. This algorithm is fast because it
implements the cone filter by using a lookup table. The lookup table
returns the proper intensity value for a pixel based on line thickness
and the distance of the pixel from the line.
Another way to do fast weighted area sampling is to subsample the area
covered by each pixel and use a pixel-weighting mask located at each
pixel to determine the desired pixel intensity value...
(A) Define a pixel weighting mask to approximate a cone filter
with a radius equal to 1 grid spacing. Assume that pixel intensity
values can range from 0 to 256.
Here is one approximation:
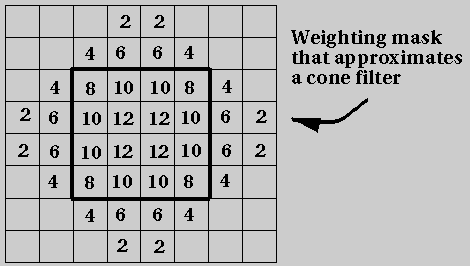
(B) Estimate the intensity value for the pixel shown above
using your filter.
The pixel intensity is set to the sum of subpixel intensities, in
this case, 78:
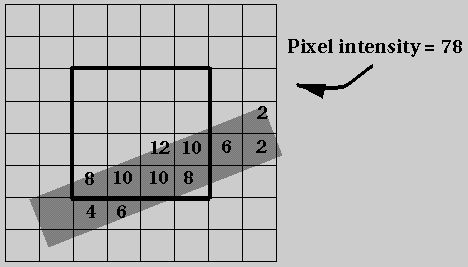
(C) What are some of the pros and cons of this approach
compared to the Gupta-Sproull algorithm?
Pros: You can create many different types of masks very easily, by
simply adjusting the weighting applied to each subpixel. This would
allow control, for example, over the amount of blur added to an
image.
Cons: The major disadvantage is that pixel subsampling is
computationally expensive.
- The midpoint scan line algorithm has the problem that intensity
of the resulting lines appears to vary by slope.
(A) Why does this occur?
When the midpointLine algorithm is used, the number of pixels
highlighted for a line depends only on the number of rows or the
number of columns spanned by that line. For lines with |slope| <= 1,
for example, the number of pixels highlighted depends on
(xmax - xmin). Lines that are at a 45 degree
angle will have the same number of pixels highlighted
as horizontal lines having endpoints at the same x values. The 45
degree line, however, will be sqrt(2) times as long as the horizontal
line. The pixels of the angled line will be more stretched out,
making the line appear dimmer.
(B) Does weighted area sampling fix the problem? Why or why
not?
Unweighted area sampling is sufficient to fix this problem by
making intensity of the line proportional to the area covered by that
line and thus proportional to its length.
Weighted area sampling has a similar effect, because the area of
overlap of a pixel with the line is used in computing pixel intensity.
There will be some variation in intensity of a line, depending on the
exact location and angle of the line, but this variation will be very
small compared to that introduced by the midpoint scan line algorithm.
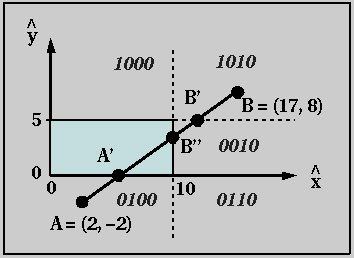
- Use the Cohen-Sutherland clipping algorithm (described in class
and in the text) to clip line AB to the 10x5 window shown in the
figure. Write down all your steps.
- Determine codes for points A and B:
- A = 0100
- B = 1010
- Test (A AND B) = (0100 AND 1010) = 0000. Because the result is
0000, the line segment cannot be trivially rejected.
- Solve for a, b, and c in the line equation ax + by + c = 0.
Plug
in endpoints:
- a(2) + b(-2) + c = 0
- a(17) + b(8) + c = 0
Subtract the first equation from the second:
- 15a + 10b = 0
- b = -1.5a
Plug this result into the first equation:
- a(2) + (-1.5a)(-2) + c = 0
- c = -5a
Set a=10 to obtain integer values:
- a = 10
- b = -1.5a = -15
- c = -5a = -50
The line equation is:
- 10x - 15y - 50 = 0
- Examine A = 0100. The 1 indicates that A should be clipped at its
intersection with the bottom of the clip window. Compute this
intersection to obtain A' as shown below. Line AB is intersected with
the line (y = 0) as follows:
- 10x - 15(0) - 50 = 0
- x = 5
- A' = (5, 0)
- Determine the code for A':
- A' = 0000
- Test (A' AND B) = (0000 AND 1010) = 0000. Because the result is
0000, the line segment cannot be trivially rejected.
- Examine A' = 0000. There are no 1 values in this code, so A' is
ok.
- Examine B = 1010. The high order 1 indicates that B should be
clipped at its intersection with the top of the clip window. Compute
this intersection to obtain B' as shown below. Line AB is intersected
with the line y=5 as follows:
- 10x - 15(5) - 50 = 0
- x = 12.5
- B' = (12.5, 5)
- Determine the code for B':
- B' = 0010
- Test (A' AND B') = (0000 AND 0010) = 0000. Because the result is
0000, the line segment cannot be trivially rejected.
- Examine B' = 0010. The 1 indicates that B should be
clipped at its intersection with the right of the clip window. Compute
this intersection to obtain B'' as shown below.Line AB is intersected
with the line x=10 as follows:
- 10(10) - 15y - 50 = 0
- y = 10/3
- B'' = (10, 10/3)
- Determine the code for B'':
- B'' = 0000
- Test (A' AND B'') = (0000 AND 0000) = 0000. Because the result is
0000, the line segment cannot be trivially rejected.
- Examine B'' = 0000. There are no 1 values in this code, so B'' is
ok.
- Accept line segment A'B'' from (5, 0) to (10, 10/3).
- The Sutherland-Hodgeman polygon clipping algorithm (also
described in class and in the text) works by clipping a polygon
against infinite lines passing through each of the window edges in
succession.
(A)Draw the four stages of the Sutherland-Hodgeman clipping
algorithm as the polygon shown below is clipped by the right, top,
left, and bottom clipping planes. Number the vertices of the polygon
in counterclockwise order at each stage.
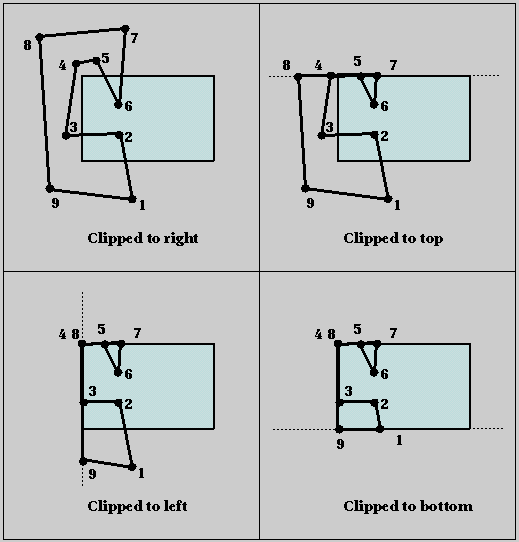
(B)The result has extra edges. Describe an algorithm for
cleaning up these extra edges to create two separate polygons.
Here is one possible algorithm, based on identifying independent
loops.
- Merge vertices that are duplicated. This just cleans up
the list of vertices by giving a unique identifier to each vertex.
In this case, merge vertices 4 and 8 and call it vertex m. The
polygon vertex loop is now:
- 1 2 3 m 5 6 7 m 9 /* start */
- Add vertices everywhere they appear.This gives us handles
at which to clip off independent polygons. The basic idea is to add a
vertex to the vertex loop at any point where it is crossed by some
edge. This gives us a new vertex loop:
- 1 2 3 m 5 6 7 5 m 3 9 /* all vertex crossings */
- Form all possible polygons. Any time a vertex repeats,
(here vertices 3 and 5), two separate polygons can be created by
removing portions of the loop between the two repeated vertices. For
example, the loop "5 6 7 5" is redundant and can be replaced simply by
"5" to yield "1 2 3 m 5 m 3 9." Similarly, starting from the last
part of the original loop and continuing around, we see that the loop
"5 m 3 9 1 2 3 m 5" is also redundant and can be replaced by "5" to
yield "5 6 7." Each of these new, smaller loops represents a potential
good polygon. Here is the complete list:
- 1 2 3 m 5 6 7 5 m 3 9 /* all vertex crossings */
- 3 m 5 6 7 5 m /* clip at 3 (top portion) */
- 1 2 3 9 /* clip at 3 (bottom portion) */
- 5 6 7 /* clip at 5 (top portion) */
- 1 2 3 m 5 m 3 9 /* clip at 5 (bottom portion) */
- 1 2 3 m 3 9 /* clip at m (bottom portion) */
- m 5 6 7 5 /* clip at m (top portion) */
- Throw out polygons with repeated vertices. A polygon
with a repeated vertex will be degenerate in some way. If all of the
polygons with repeated vertices are discarded, only the following
remain:
- 1 2 3 9 /* clip at 3 (bottom portion) */
- 5 6 7 /* clip at 5 (top portion) */
These are the polygons we want.